Deret Geometri: Pengertian, Rumus, Contoh Soal

Deret geometri merupakan salah satu materi yang diajarkan di sekolah. Berikut ini penjelasan mengenai konsep deret geometri.

Perhatikan deret bilangan berikut.

3 + 9 + 27 + … + 729

Berapakah jumlah suku-suku pada deret bilangan tersebut? Untuk menentukan jumlah suku-suku tersebut, kalian harus mempelajari materi deret geometri.

Pada artikel ini akan dibahas mengenai pengertian deret geometri beserta contoh penerapannya, rumus deret geometri, deret geometri tak hingga, serta menentukan rumus jumlah n suku pertama deret geometri.

Oke, kita mulai dari pengertian deret geometri berikut.

Pengertian Deret Geometri

Deret geometri dapat disebut sebagai jumlah dari barisan bilangan yang suku-sukunya membentuk barisan geometri, sehingga deret geometri mudah untuk dibedakan dari yang lainnya.

Pada deret geometri, suku-sukunya memiliki rasio yang tetap. Rasio adalah perbandingan antar suku-suku pada deret tersebut.

Misalnya perbandingan antara suku kedua dengan suku pertama akan sama dengan suku ketiga dengan suku kedua, begitu pula yang lainnya.

Berikutnya akan dijelaskan mengenai contoh penerapan deret geometri.

Contoh Penerapan Deret Geometri

Deret geometri dapat diterapkan pada penghitungan panjang lintasan dari bola yang dijatuhkan lalu bola tersebut memantul hingga berhenti.

Rasio dari deret tersebut yaitu perbandingan antara tinggi pantulan pertama dengan tinggi awal bola dijatuhkan atau tinggi pantulan kedua dengan tinggi pantulan pertama, dan seterusnya.

Pada bagian berikutnya akan dijelaskan mengenai rumus deret geometri.

Rumus Deret Geometri

Deret geometri disimbolkan dengan S_n. Deret geometri dapat dirumuskan sebagai:

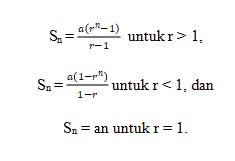
Keterangan:

• S_n : jumlah suku pada deret geometri
• a : suku pertama pada deret geometri
• r : rasio pada deret geometri
• n : banyaknya suku pada deret geometri

Berikutnya akan dijelaskan mengenai deret geometri tak hingga.

Deret Geometri Tak Hingga

Deret geometri tak hingga merupakan deret geometri yang memiliki tak hingga banyak suku atau banyak sukunya mendekati tak hingga (infinite). Perhatikan contoh deret geometri tak hingga berikut.

3 + 1 + 1/3 + 1/9 + …

Deret tersebut memiliki rasio yang tetap yaitu r = 1/3 dan memiliki tak hingga banyak suku sehingga disebut sebagai deret geometri tak hingga.

Untuk menentukan jumlah suku dari deret geometri tak hingga dapat menggunakan rumus deret geometri tak hingga berikut ini.

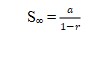
Keterangan:

• S_∞ : jumlah suku pada deret geometri tak hingga
• a : suku pertama deret geometri tak hingga
• r : rasio deret geometri tak hingga

Selanjutnya akan disampaikan penjelasan mengenai menentukan rumus jumlah n suku pertama deret geometri.

Rumus Jumlah n Suku Pertama Deret Geometri

Misalkan terdapat deret geometri sebagai berikut.

3 + 6 + 12 + 24 + …

Cara menentukan jumlah n suku pertama deret geometri tersebut yaitu:

1. Menentukan suku pertama (a).

a = 3

2. Menentukan rasio deret tersebut (r).

r = U₂/U₁ = 6/3 = 2

3. Substitusi nilai a dan r pada rumus deret geometri.

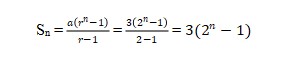
Setelah kalian memahami penjelasan mengenai deret geometri tersebut, berikut ini terdapat contoh soal dan pembahasan deret geometri.

Contoh Soal Deret Geometri

1. Diketahui suatu deret sebagai berikut.

6 + 18 + 54 + …

Berapakah jumlah 8 suku pertama deret tersebut?

Pembahasan

Deret bilangan tersebut merupakan deret geometri dengan a = 6 dan r = 3.

Sehingga jumlah 8 suku pertama deret tersebut yaitu:

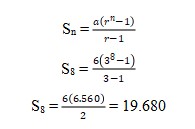
Jadi, jumlah 8 suku pertama deret tersebut adalah 19.680.

2. Diketahui deret geometri tak hingga sebagai berikut.

4 + 2 + 1 + ½ + …

Jumlah deret geometri tak hingga tersebut adalah ….

Pembahasan

Deret geometri tak hingga tersebut memiliki a = 4 dan r = 1/2 .

Sehingga:

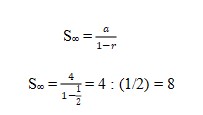
Jadi, jumlah deret geometri tak hingga tersebut adalah 8.

Demikian penjelasan mengenai deret geometri. Semoga bermanfaat dan tetap semangat belajar.