Pada artikel kali ini akan dibahas mengenai barisan geometri.
Pernahkah kalian menjumpai barisan bilangan? Barisan bilangan seperti apa yang kalian lihat?
Dalam kehidupan sehari-hari kita sering melihat berbagai bilangan. Beberapa dari bilangan-bilangan tersebut ada yang membentuk barisan bilangan.
Misalnya 2, 4, 6, 8, … . Barisan bilangan tersebut disebut sebagai barisan bilangan genap. Mengapa barisan bilangan tersebut disebut sebagai barisan bilangan genap? Karena setiap sukunya dapat dibagi dengan bilangan 2 (genap).
Ada juga barisan lainnya yang disebut dengan barisan geometri. Untuk lebih memahami mengenai barisan geometri, pahami penjelasan berikut ini.
Pengertian Barisan Geometri
Pada bagian sebelumnya, kalian telah diberikan contoh barisan bilangan. Berbagai jenis barisan bilangan memiliki karakteristik atau ciri tertentu yang membedakannya dengan barisan bilangan lainnya.
Barisan geometri merupakan barisan yang memiliki rasio antar sukunya. Misalnya pada barisan geometri berikut ini.
3, 6, 12, 24, 48, …
Barisan bilangan tersebut merupakan barisan geometri dengan rasio 2.
Bagian selanjutnya akan dibahas mengenai contoh penerapan bsarisan geometri.
Contoh Penerapan Barisan Geometri
Barisan geometri banyak diterapkan dalam kehidupan sehari-hari. Barisan geometri dapat dimanfaatkan untuk menghitung ketinggian pantulan bola yang dijatuhkan dari ketinggian tertentu.
Bola yang dijatuhkan pada ketinggian tertentu tersebut, tinggi pantulannya akan membentuk barisan geometri dengan rasio tertentu.
Berikutnya akan diuraikan terkait rumus yang digunakan pada barisan geometri.
Rumus Barisan Geometri
Rumus barisan geometri untuk menentukan suku ke-n yaitu sebagai berikut.
Un = a . rn-1
Keterangan:
- Un : suku ke-n barisan geometri’
- a : suku pertama barisan geometri
- r : rasio barisan geometri
- n : banyaknya suku pada barisan geometri
Berikutnya akan dijelaskan mengenai suku tengah dan suku sisipan pada barisan geometri.
Suku Tengah Barisan Geometri
Suku tengah barisan geometri hanya dapat ditentukan pada barisan geometri dengan banyak suku ganjil (n ganjil). Misalnya pada barisan bilangan yang terdiri dari 3 suku berikut.
2, 6, 18
Suku tengah barisan geometri tersebut adalah 6. Bagaimana jika barisan geometri memeiliki suku yang sangat banyak? Untuk menentukan suku tengahnya perhatikan penjelasan berikut.
Terdapat barisan dengan banyak sukunya ganjil:
U1, U2, . . . . U2k-1
Suku tengah barisan geometri dapat dirumuskan sebagai:
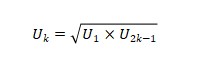
Keterangan:
- Uk : suku tengah barisan geometri
- U1 : suku pertama barisan geometri
- U2k-1 : suku ganjil terakhir dari barisan geometri
Berikutnya aka dijelaskan mengenai suku sisipan pada barisan geometri.
Suku Sisipan pada Barisan Geometri
Terdapat suatu barisan geometri. Jika di antara dua suku (missal a dan b) disisipkan sebanyak bilangan, maka rasio barisan geometri yang baru yaitu:
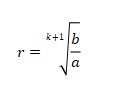
Keterangan:
- r : rasio barisan geometri yang baru
- k : banyaknya suku sisipan
- a dan b : dua suku berurutan pada barisan geometri sebelumnya.
Setelah memahami konsep barisan geometri, pahami beberapa soal berikut untuk menguji pemahamanmu mengenai barisan geometri.
Contoh Soal Barisan Geometri
1. Suku kedua dan suku kelima dalam barisan geometri berturut-turut yaitu 3 dan 24. Tentukan suku ke-7 dari barisan tersebut.
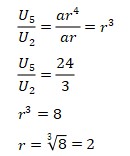
Suku ke-7 yaitu:
Un = a . rn-1
U7 = a . r6
U7 = a . r4 . r2
U7 = 24 . 4 = 96
Jadi, suku ke-7 barisan geometri tersebut adalah 96.
2. Terdapat 5 suku dalam suatu barisan geometri dengan suku pertama 2 dan suku terakhirnya 162. Suku tengah barisan tersebut adalah ….
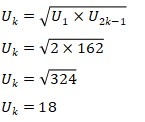
Jadi, suku tengah barisan tersebut adalah 18.
3. Suatu barisan suku pertama dan suku keduanya yaitu 4 dan 324. Jika diantara kedua suku tersebut disisipkan 3 bilangan sehingga terbentuk barisan geometri yang baru, kemungkinan rasio barisan geometri yang baru adalah ….
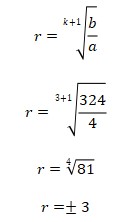
Jadi, kemungkinan rasio barisan geometri yang baru adalah -3 atau 3.
Itu tadi pembahasan mengenai barisan geometri. Semoga informasi yang disampaikan memberikan tambahan pengetahuan bagi kalian semua. Terima kasih.
