Contoh Soal Induksi Matematika dan Pembahasannya

Dalam mengerjakan soal induksi matematika, terdapat dua cara yaitu mencari basis induksi dan langkah induksi. Sebelum menyentuh basis induksi, kita harus menuliskan model matematika dari persoalan di atas.

F(x,y) = 20000x + 30000y ; dimana setiap x dan y adalah bilangan cacah

F(x,y) =10000(2x+3y)

F(x,y) = 10000(2(x+y)+y)

Bentuk terakhir dari f(x,y) menunjukkan sebuah makna yaitu suku pertama 2(x+y) bernilai genap sedangkan suku kedua y bernilai ganjil atau genap. Sehingga kita dapat mengetahui bahwa 2(x+y)+y merupakan anggota bilangan cacah. Kemudian, kita anggap 2(x+y)+y adalah n, maka persamaan baru menjadi

20000x+30000y = 10000n

Kemudian kita melakukan substitusi n. Jika n=1, tidak ditemukan nilai x dan y adalah cacah. Namun jika kita memasukkan n=2, maka didapatkan nilai x=1 dan y=0. Sehingga, persamaan tersebut akan menghasilkan x dan y jika n≥2. Pada persamaan tersebut menunjukkan jika 10000 merupakan kelipatan pada mesin ATM.

Sehingga basis induksi telah selesai. Selanjutnya, kita menerapkan metode langkah induksi. Kita dapat melakukan pemisalan n = k.

F(k): 2x + 3y = k, k≥2

Asumsi bahwa F(k) benar, maka F(k+1) juga benar. Sehingga terbukti benar bahwa f(k): 2x + 3y = k, k≥2. Sehingga, uang paling kecil yang bisa diambil minimal 20000.

Untuk mengerjakan soal ini, Kita dapat menggunakan sifat proposisi. Sehingga bentuk di atas akan seperti ini.

P_n = jika 0 < a < 2, maka 0 < aⁿ < 2

Kita dapat mencoba n sembarang nilai untuk membuktikan nilai tersebut, kita ambil n=1.

P_n = jika 0 < a < 2, maka 0 < a¹ = a < 2

Sehingga pernyataan di atas adalah benar untuk n = 1. Kita dapat melanjutkan ke langkah selanjutnya yaitu langkah induksi.

P_n = jika 0 < a < 2, maka 0 < aⁿ < 2

Kita harus mencoba menguji kebenaran P_k dan P_k+1. Jika P_k benar, maka P_k+1 benar.

P_n = jika 0 < a < 2, maka 0 < a^k < 2

P_n = jika 0 < a < 2, maka 0 < a^k+1 < 2

Dalam sebuah dijelaskan jika 0<a<b, maka 0<ax<by. Maka a^k+1 sebagai berikut

0 < a.a^k < 2 x 1 ↔ 0 < a^k+1 < 2

Sehingga 0 < a^k+1 < 2 adalah benar. Artinya, P_k benar, maka P_k+1 juga benar. 

Kita memasukkan nilai n=0 maka, P₀=1. Kita dapat buktikan dengan cara memasukkan nilai 0 ke dalam persamaan 2ⁿ⁺¹-1.

P_{0 :} 2⁰⁺¹-1 = 1, pernyataan tersebut benar.

Kemudian, kita coba masukkan nilai k dan k+1 pada fungsi deret di atas.. Diasumsikan jika P_k benar maka P_k+1 benar. Maka kita harus menguji ruas kanan dan ruas kiri.  

P_k+1 : 2⁰+2¹+2²+2³+….+2^k+1 = 2^k+2-1

P_k+1 : 2^k+1 -1 + 2^{k+1 = 2.} 2^k+1 – 1

P_k+1 = 2^k+2 – 1

Terbukti bahwa P_k benar maka P_k+1 juga benar.

Seperti pada soal sebelumnya, kita dapat melakukan pemisalan dengan nilai n=1. Sehingga nilai P₁: 1² = 1. Hal ini menandakan jika persamaan tersebut benar untuk n=1. Langkah selanjutnya adalah menguji nilai n=k dan n=k+1.

Dengan mengasumsikan jika P_k = k² adalah benar. Maka P_k+1 = (k+1)² juga benar. Kita harus memastikan ruas kiri dan ruas kanan adalah sama

P_k+1 = 1+3+5+7+…+(2k-1)+(2k+1)

P_k+1 = k² + 2k + 1
P_k+1 = (k+1)²

Pernyataan tersebut benar, sehingga P_k benar dan P_k+1 benar.

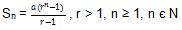
Kita dapat langsung mensubtitusikan 1 ke dalam Sn sehingga di dapatkan nilai

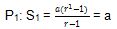
Sehingga, pernyataan benar untuk n=1. Kemudian kita dapat menguji kebenaran P_k+1 dan P_k

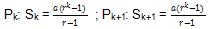
Kita dapat menguji kebenaran hasil dengan menunjukkan nilai ruas kiri dan ruas kanan.

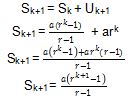
Hasilnya adalah benar. Sehingga P_k+1 dan P_k adalah benar. Dapat disimpulkan rumus tersebut adalah benar.