Pengertian
Nilai mutlak atau modulus adalah nilai suatu bilangan riil tanpa adanya tanda tambah (+) atau kurang (–).
Misalnya, nilai mutlak dari 2 sama dengan nilai mutlak dari -2 yaitu 2 atau secara umum dapat ditulis dengan |2| = |-2| = 2.
Dari sudut pandang geometri mengenai konsep jarak, nilai mutlak berarti jarak yang ditempuh tanpa memperhatikan arah. Perhatikan garis bilangan di bawah ini:
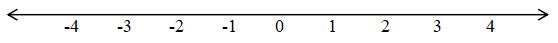
Cobalah bayangkan seseorang berdiri di titik 0, maka jika dia berjalan ke kanan sejauh 4 satuan, maka dia berada di titik 4.
Sebaliknya, jika berjalan ke kiri sejauh 4 satuan maka dia akan berada di titik -4.
Dalam hal ini, dikatakan orang tersebut berjalan sejauh 4 satuan tanpa memperhatikan tanda plus maupun minus.
Kemudian, bentuk nilai mutlak secara umum adalah seperti di bawah ini:
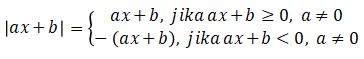
Selain bentuk umum, nilai mutlak juga memiliki sifat-sifat seperti berikut ini:

Biar lebih jelas, sobat pintar sekalian bisa nonton video rumus pintar ya
Persamaan Nilai Mutlak
Setelah kita belajar bentuk umum dan sifat-sifat nilai mutlak, sekarang akan dibahas terkait persamaan nilai mutlak yang mana “persamaan” itu sendiri ditandai dengan menggunakan tanda sama dengan (=).
Biasanya, sebuah soal persamaan nilai mutlak akan meminta kita untuk mencari himpunan penyelesaian dari persamaan tersebut menggunakan aljabar dan sifat-sifat yang ada pada nilai mutlak.
Agar materi persamaan nilai mutlak dapat lebih dimengerti, perhatikan contoh soal di bawah ini beserta dengan penyelesaiannya.
Contoh soal
Carilah himpunan penyelesaian dari |x + 1| = 2x – 3.
Jawab:
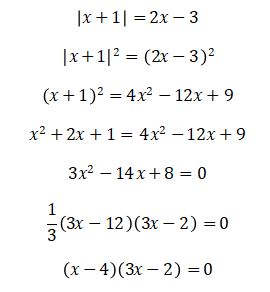
Jadi, himpunan penyelesaiannya adalah x = 4 atau x = ⅔. Baca juga Bilangan Bulat.
Sudah paham belum? Kalo belum yakin, belajar lagi di video rumus pintar tentang persamaan nilai mutlak ya.
Pertidaksamaan Nilai Mutlak
Selanjutnya akan kita bahas tentang pertidaksamaan nilai mutlak. Berbeda dari persamaan, pertidaksamaan ditandai dengan tanda kurang dari (<), kurang dari atau sama dengan (≤), lebih dari (>), atau lebih dari atau sama dengan (≥).
Sama halnya denga persamaan nilai mutlak, sebuah soal pertidaksamaan nilai mutlak biasanya meminta kita untuk mencari himpunan penyelesaian dari pertidaksamaan tersebut.
Namun perlu digaris bawahi bahwa dalam penghitungan sebuah pertidaksamaan kita harus lebih berhati-hati dan tidak boleh asal membagi kedua ruas seperti saat mengerjakan soal persamaan, karena tanda dari pembagi (plus atau minus) dapat membuat tanda dari sebuah pertidaksamaan menjadi kebalikannya.
Agar lebih mudah dimengerti, perhatikan penjelasan dari video di bawah ini:
Contoh Soal Nilai Mutlak
Untuk lebih memahami tentang konsep nilai mutlak, mari kita pelajari kumpulan contoh soal nilai mutlak beserta jawaban dan pembahasannya yang sudah kami kumpulkan di bawah ini. Mari kita pelajari bersama soal-soal berikut.
1. Tentukanlah Himpunan penyelesaian dari |3x + 1| = |x – 5| !
|3x + 1| = |x – 5|
3x + 1 = x – 5 atau 3x + 1 = – (x – 5)
3x + 1 = x – 5
3x – x = –5 – 1
2x = –6
x = –3
Atau
3x + 1 = – (x – 5)
3x + 1 = – x + 5
3x + x = 5 – 1
4x = 4
x = 1
Jadi, Himpunan penyelesaian dari |3x + 1| = |x – 5| adalah {–3, 1}.
2. Cari himpunan penyelesaian dari |2x – 5| = 7
|2x – 5| = 7
2x – 5 = 7 atau 2x – 5 = –7
2x – 5 = 7
2x = 7 + 5
2x = 12
x = 6
Atau
2x – 5 = –7
2x = –7 + 5
2x = –2
x = –1
Jadi, himpunan penyelesaian dari |2x – 5| = 7 adalah {–1, 6}.
3. Temukan himpunan penyelesaian |6x – 3 | ≥ 9
|6x – 3 | ≥ 9
6x – 3 ≤ –9 atau 6x – 3 ≥ 9
6x – 3 ≤ –9
6x ≤ –9 + 3
6x ≤ –6
x ≤ –1
atau
6x – 3 ≥ 9
6x ≥ 9 + 3
6x ≥ 12
x ≥ 2
Jadi, himpunan penyelesaian |6x – 3 | ≥ 9 adalah {x | x ≤ –1 atau x ≥ 2}.
4. Tentukan himpunan penyelesaian dari |2x – 7| ≥ |3x + 2|
|2x – 7| ≥ |3x + 2|
2x – 7 ≥ 3x + 2 atau 2x – 7 ≤ – (3x + 2)
2x – 7 ≥ 3x + 2
– 7 – 2 ≥ 3x – 2x
–9 ≥ x
x ≤ –9
Atau
2x – 7 ≥ – (3x + 2)
2x – 7 ≥ – 3x – 2
2x + 3x ≥ – 2 + 7
5x ≥ 5
x ≥ 1
Jadi, himpunan penyelesaian dari |2x – 7| ≥ |3x + 2| adalah {x | x ≤ –9 atau x ≥ 1}.
5. Cari himpunan penyelesaian dari |2x – 3| < 5
|2x – 3| < 5
–5 < 2x – 3 < 5
–5 + 3 < 2x < 5 + 3
–2 < 2x < 8
–1 < x < 4
Jadi, himpunan penyelesaian dari |2x – 3| < 5 adalah {x | –1 < x < 4}.
6. Temukan himpunan penyelesaian dari 2|x – 5| + 3 = 17
2|x – 5| + 3 = 17
2|x – 5| = 17 – 3
2|x – 5| = 14
|x – 5| = 14 ÷ 2
|x – 5| = 7
x – 5 = 7 atau x – 5 = – 7
x – 5 = 7
x = 12
Atau
x – 5 = – 7
x = –2
Jadi, himpunan penyelesaian dari 2|x – 5| + 3 = 17 adalah {–2, 12}.
7. Tentukan himpunan penyelesaian dari |5 – 2x| – 8 ≤ 7 !
|5 – 2x| – 8 ≤ 7
|5 – 2x| ≤ 7 + 8
|5 – 2x| ≤ 15
– 15 ≤ 5 – 2x ≤ 15
– 15 – 5 ≤ –2x ≤ 15 – 5
– 20 ≤ –2x ≤ 10
10 ≥ x ≥ –5 (semua ruas dikalikan angka negatif –½, tanda pertidaksamaan berubah)
– 5 ≤ x ≤ 10
Jadi, himpunan penyelesaian dari |5 – 2x| – 8 ≤ 7 adalah {x | – 5 ≤ x ≤ 10}.
8. Himpunan penyelesaian dari |x – 2| < 3x adalah…
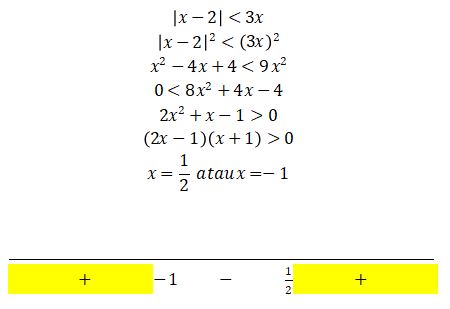
Jadi, himpunan penyelesaian dari pertidaksamaan di atas adalah x < -1 atau x > ½
2. Jika – 7 < x < 2, maka nilai x yang memenuhi 5 |x+7| + x |x-2| < 35 adalah…

Jadi, himpunan penyelesaian dari (2) adalah x < 0 atau x > 7.
Dari (1) dan (2) didapatkan himpunan penyelesaian bersama yaitu -7 < x < 0.
Setelah kita mempelajari persamaan dan pertidaksamaan nilai mutlak, dapat kita simpulkan bahwa keduanya sama-sama mencari himpunan penyelesaian.
Perbedaannya adalah himpunan penyelesaian sebuah persamaan nilai mutlak bersifat diskrit (titik) sedangkan sebuah pertidaksamaan nilai mutlak bersifat kontinu (interval).
Dengan demikian, perbedaan itu pula yang akan mendasari perbedaan dari persamaan dan pertidaksamaan nilai mutlak.
