Pernahkah kalian bermain monopoli? Untuk dapat bermain monopoli, kalian harus melemparkan dadu, angka yang kemudian muncul merupakan jumlah jalan yang harus ditempuh oleh pelempar dadu.
Pelemparan dadu bermata 6 pada permainan monopoli ini akan menghasilkan angka 1, 2, 3, 4, 5, atau 6.
Kemungkinan keluarnya angka tertentu pada pelemparan dadu bermata 6 adalah satu contoh dari banyak contoh penerapan materi matematika peluang dalam kehidupan sehari-hari.
Contoh lain dari peluang pada kehidupan sehari hari adalah pelemparan uang koin.
Pada saat melemparkan koin, ada dua buah kemungkinan mengenai sisi yang muncul. Sisi yang pertama adalah sisi angka dan sisi yang kedua adalah sisi gambar.
Nah, kali ini materi yang akan kita bahas adalah mengenai peluang. Mari kita simak materi berikut ini.
Definisi Peluang Matematika
Peluang pada umumnya berarti kesempatan, namun pada matematika, peluang atau probabilitas adalah kemungkinan yang mungkin terjadi/muncul dari suatu peristiwa.
Terkadang kita mengukur sebuah peluang dengan angka, seperti “kemungkinannya sekitar 10%”, atau dengan perkataan, seperti, “ah itu tidak mungkin” atau “itu sudah pasti terjadi”.
Dalam angka, peluang selalu berkisar antara 0 sampai dengan 1. Dimana 0 menyatakan sebuah kejadian yang tidak mungkin terjadi dan 1 menyatakan sebuah kejadian yang pasti terjadi, dalam matematika hal ini dinotasikan sebagai
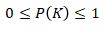
dengan P(K) menyatakan peluang terjadinya kejadian K.
Istilah yang Sering Digunakan
Di dalam materi peluang, ada beberapa istilah yang sering digunakan, diantaranya
Ruang sampel : Himpunan dari semua hasil percobaan yang mungkin terjadi
Titik sampel : Anggota dari ruang sampel
Kejadian : Himpunan bagian dari ruang sampel
Rumus Peluang
Sebelum membahas rumus peluang, terlebih dahulu kita akan membahas mengenai frekuensi relatif.
Frekuensi relatif adalah perbandingan dari banyak percobaan yang dilakukan dengan banyaknya kejadian yang diamati.
Frekuensi relatif dapat dicari dengan menggunakan rumus
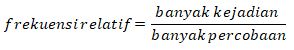
Apabila peluang dari setiap titik sampel dari anggota ruang sampel S sama, maka peluang kejadian K yang jumlah anggotanya ditulis sebagai n(K) dapat dicari dengan rumus
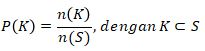
Contoh Soal
Pada pelemparan sebuah dadu, tentukan peluang munculnya sisi dadu yang berangka genap
Ruang sampel S adalah {1,2,3,4,5,6}
n(S) = 6
Sisi dadu genap adalah {2,4,6}
n(K) = 3
maka
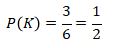
jadi, peluang munculnya mata dadu berangka genap adalah 0,5.
Kejadian Majemuk
Kejadian majemuk adalah kejadian baru yang terbentuk dari perlakuan pada dua atau lebih kejadian.
Kejadian Komplemen
Kejadian K komplemen adalah semua kejadian yang bukan kejadian K. Suatu kejadian K dan kejadian K komplemen (yang dinyatakan K’) memenuhi
P(K) + P(K’) = 1 atau P(K’) = 1 – P(K)
Contoh soal:
Ana bermain kartu bridge, kemudian diambil satu kartu secara acak. Tentukan peluang Ana mengambil kartu bukan As
jumlah semua kartu bridge
n (S) = 52
jumlah semua kartu As
n(K) = 4
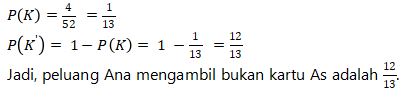
Penjumlahan Peluang
Kejadian saling lepas
Terdapat dua buah kejadian A dan B yang kemudian disebut kejadian saling lepas jika tidak ada elemen pada kejadian A yang sama dengan elemen yang terdapat pada kejadian B.
Peluang salah satu A atau B mungkin terjadi dengan A dan B adalah kejadian saling lepas, rumusnya adalah
P(A Ս B) = P(A) + P (B)
Contoh Soal
Terdapat dua buah dadu, biru dan hijau. Dua dadu tersebut kemudian dilempar secara bersamaan satu kali, tentukan peluang munculnya sisi dadu yang memiliki jumlah 3 atau 10!
Hasil pelemparan dadu tersebut kemudian dituliskan dalam tabel dibawah ini
| Dadu | Merah | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) | |
| Dadu | 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| Biru | 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) | |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) | |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
Munculnya mata dadu berjumlah 3
A = {(1,2), (2,1)}
n(A) = 2
Munculnya mata dadu berjumlah 10
B = {(4,6), (5,5), (6,4)}
Karena anggota A tidak ada yang sama dengan anggota B, maka kejadian A dan B merupakan dua kejadian yang saling lepas sehingga menggunakan rumus:

sehingga peluang munculnya mata dadu yang berjumlah 3 atau 10 adalah .
Kejadian tidak saling lepas
Dua buah kejadian A dan B disebut tidak saling lepas jika terdapat minimal satu elemen pada kejadian A yang sama dengan elemen yang terdapat pada kejadian B. Peluang salah satu A atau B mungkin terjadi dengan A dan B adalah kejadian tidak saling lepas, rumusnya adalah
P(A Ս B) = P(A) + P (B) – P(A Ո B)
Dimana P(A Ո B) menyatakan elemen yang terdapat pada kejadian A dan B
Contoh Soal
Doni sedang bermain kartu bridge, kemudian Ia mengambil satu kartu secara acak. Tentukan peluang kartu yang diambil adalah kartu sekop dan kartu bergambar (J,Q,K)!
Jumlah kartu bridge
n(S) = 52
jumlah kartu sekop
n(A) = 13
jumlah kartu bergambar
n(B) = 12
karena terdapat kartu bergambar yang merupakan anggota kartu sekop (J sekop, Q sekop, dan K sekop) maka A dan B merupakan dua kejadian tidak saling lepas sehingga digunakan rumus:

Jadi, peluang dari kartu yang terambil adalah kartu sekop dan kartu bergambar (J,Q,K) adalah .
Kejadian saling bebas
Dua buah kejadian A dan B dikatakan saling bebas jika munculnya kejadian A tidak mempengaruhi kejadian B. Peluang kejadian A dan B terjadi bersama sama adalah
P(A Ո B) = P(A) × P(B)
Contoh Soal
Andi melempar dua buah dadu, berapakah peluang muncul angka genap prima pada dadu pertama dan angka ganjil pada dadu kedua!
misalkan A = kejadian muncul mata dadu genap prima pada dadu pertama
A={2}, maka P(A) = 1/6
misalkan B = kejadian muncul mata dadu ganjil pada dadu kedua = {1,3,5} maka P(B) = 3/6
Kejadian A tidak mempengaruhi kejadian B, maka digunakan rumus:
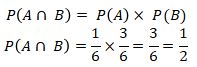
Jadi, peluang muncul angka genap prima pada dadu pertama dan angka ganjil pada dadu kedua adalah 0,5.
Kejadian bersyarat
Jika terdapat dua kejadian yaitu kejadian A dan kejadian B, kejadian tersebut dikatakan kejadian bersyarat jika kejadian A mempengaruhi terjadinya kejadian B atau sebaliknya, kemudian dapat dituliskan sebagai berikut ini
P(A Ո B) = P(A) × P(B|A)
Atau
P(A Ո B) = P(B) × P(A|B)
Contoh Soal
Terdapat kotak yang memuat 5 bola kuning dan 4 bola biru. Jika diambil dua buah bola, secara satu persatu dan tanpa ada pengembalian, maka berapakah peluang bola yang diambil adalah bola kuning pada pengambilan pertama dan bola biru pada pengambilan kedua!
Pada pengambilan pertama tersedia 5 bola kuning dari 9 bola yang tersedia.
Maka P(K) = 5/9
Pada pengambilan kedua tersedia 4 bola biru dari 8 bola yang tersisa (syarat : bola kuning telah diambil).
Maka P(B|K) = 4/8
karena kejadian tersebut saling mempengaruhi, kemudian digunakanlah rumus:
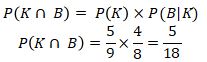
Jadi, peluang bola yang terambil adalah bola merah pada pengambilan pertama dan bola hijau pada pengambilan kedua adalah 5/18.
Contoh Soal Peluang
Terdapat wadah P, ada 8 kelereng merah dan 5 kelereng putih di dalamnya. Wadah O, terdapat 7 kelereng merah dan 8 kelereng hitam di dalamnya. Kemudian, diambil satu kelereng secara acak dari wadah P dan O. Peluang terambilnya kelereng putih dari wadah P dan kelereng hitam dari wadah O adalah..
Untuk mengerjakan soal pertama, kita harus membuat peluang pada masing-masing wadah. Kemudian, informasi yang diberikan oleh soal adalah penggunaan kata ‘dan’ sehingga peluang yang terjadi pada wadah P dan wadah O akan dikalikan seperti penyelesaian di bawah ini.
Wadah P: Besar peluang kelereng putih = P(P) = 5/13
Wadah O: Besar peluang kelereng hitam = P(O) = 8/15
Peluang terambilnya kelereng putih dari wadah P dan kelereng hitam dari wadah O adalah P(PO).
P(PO) = P(P) x P(O)
P(PO) = (5/13) x (8/15) = 8/39
Besar peluang terambilnya adalah 8/39 dari wadah P dan O
Wawan akan melakukan uji peluang kejadian pada dua dadu yang di lempar secara bersamaan sebanyak satu kali. Berapakah peluang kejadian munculnya jumlah kedua dadu 2 atau 8?
Dalam mengerjakan soal peluang dadu, kita harus mengetahui ruang sampel dadu. Dadu memiliki ruang sampel sebanyak 36. Untuk lebih jelasnya, bisa kita perhatikan tabel ruang sampel dadu di bawah ini.
| DADU | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
Berdasarkan soal, jika kita melempar dadu, kemungkinan munculnya angka 2 jika kedua sisi dadu memperlihatkan angka 1 seperti warna kuning pada tabel di atas. Untuk angka 8, terdapat 5 kemungkinan yaitu (2,6), (3,5), (4,4), (5,3), (6,2). Sehingga proses pengerjaannya seperti di bawah ini.
Peluang munculnya angka 2: P(2) = 1/36
Peluang munculnya angka 8: P(8) = 5/36
Peluang munculnya angka 8 atau 2: P(2) + P(8) = 1/36 + 5/36 = 6/36 = 1/6
Berapa banyak susunan yang bisa dibuat dari kata “PELUANG”?
Dalam mengerjakan soal sejenis ini, pertama, kita harus memperhatikan banyaknya huruf dalam kata “PELUANG”. Kemudian, kita harus menuliskan banyak per huruf seperti di bawah ini untuk jelasnya.
Jumlah kata dan huruf: n = 7; P = 1; E = 1; L = 1; U = 1; A = 1; N = 1; G = 1.
Banyak susunan yang bisa dibuat: P(S) = ![]() = 5040 kata
= 5040 kata

Kita bisa menggunakan materi kofaktorial pada peluang untuk mengerjakan soal ini.
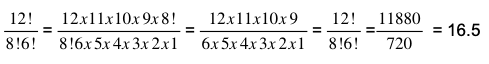
Kesimpulan

Sekian materi peluang kali ini. Semoga bermanfaat dan bertemu lagi di materi lainnya.
