Apakah kalian mencari informasi mengenai regresi? Jika iya, coba baca artikel berikut mengenai regresi.
Pernahkah kalian mempunyai sepasang data yang saling berhubungan, misalnya data usia seseorang dengan tinggi badannya?
Kedua data tersebut dapat dirumuskan fungsinya dengan metode statistika. Metode tersebut dikenal dengan regresi.
Regresi ini juga dapat meramalkan suatu nilai tertentu jika diketahui salah satu nilainya. Agar lebih memahaminya, perhatikan penjelasan mengenai pengertian regresi berikut.
Pengertian Regresi
Regresi adalah suatu metode statistik dengan merumuskan persamaan atau fungsi matematis yang menunjukkan hubungan atau pengaruh dari dua buah variabel atau lebih.
Regresi ini juga dapat digunakan sebagai suatu prediksi dengan data-data yang diolah merupakan data kuantitatif.
Berikutnya akan dijelaskan mengenai contoh penerapan regresi.
Contoh Penerapan Regresi
Regresi ini banyak diterapkan dalam berbagai bidang seperti bidang ekonomi, industri, dan lainnya.
Pada bidang ekonomi, regresi ini dapat diterapkan untuk memprediksi banyak pengeluaran tiap keluarga terhadap penghasilan per bulan.
Pada bidang industri, regresi dapat diterapkan dalam menentukan dan memprediksi harga bahan baku industri terhadap ketersediaan bahan baku industri di pasar.
Dalam bidang lainnya, regresi juga dapat diterapkan dalam memprediksi tingkat upah pekerja dengan banyaknya pengangguran.
Itulah contoh penerapan regresi dalam berbagai bidang. Selanjutnya akan diuraikan mengenai macam regresi.
Macam-Macam Regresi
Macam regresi diuraikan sebagai berikut.
1. Regresi Linear Sederhana
Regresi linear sederhana yaitu regresi yang hanya menentukan hubungan dari dua variabel saja dan keduanya merupakan data kuantitatif.
Misalnya data banyak makanan yang dikonsumsi dengan berat badan.
2. Regresi Linear Berganda
Regresi linear berganda ini merupakan regresi yang menghubungkan satu variabel Y terhadap dua atau lebih variabel X serta data yang digunakan merupakan data kuantitatif.
Misalnya pengaruh banyak makanan yang dikonsumsi terhadap berat badan dan tinggi badan.
3. Regresi Non Linear
Regresi non linear ini merupakan regresi yang menghubungkan antara variabel X dan variabel Y yang tidak linear.
Misalnya pada pemberian pupuk pada tanaman dengan intensitas pemberian pupuk rendah – sedang akan membuat tanaman tumbuh dengan optimal (tinggi tanaman maksimum), sedangkan pemberian pupuk intensitas tinggi akan membuat tanaman tumbu dengan lambat.
Berikutnya akan dijelaskan mengenai rumus regresi.
Rumus Regresi
Beberapa rumus regresi yaitu sebagai berikut.
Rumus Regresi Linear Sederhana
Bentuk umum regresi linear sederhana dituliskan sebagai:
Y = a + bX
Keterangan:
- a : konstanta (titik potong Y)
- b : koefisien dari variabel X
- Y : variabel dependen
- X : variabel independen
Rumus Regresi Linear Berganda
Bentuk umum regresi linear berganda dapat dituliskan sebagai:
Y = a + b1X1 + b2X2 + … + e
Keterangan:
- a : konstanta (titik potong Y)
- b : koefisien dari variabel X (koefisien determinasi)
- Y : variabel dependen
- X : variabel independen
- e : error
Rumus Regresi Non Linear
Beberapa contoh bentuk umum regresi non linear dituliskan sebagai berikut.
- Regresi berbentuk eksponensial: Y = aebX
- Regresi berbentuk pangkat: Y = aXb
- Regresi berbentuk polinomial: Y = a0 + a1X + … +anXn
Selanjutnya terdapat soal mengenai regresi sebagai berikut.
Contoh Soal Regresi
Berikut ini merupakan data penghasilan dan pengeluaran suatu keluarga.
| No. | Penghasilan (juta rupiah) | Pengeluaran (juta rupiah) |
| 1 | 19 | 10 |
| 2 | 14 | 8 |
| 3 | 14 | 7 |
| 4 | 10 | 7 |
| 5 | 13 | 8 |
| 6 | 16 | 9 |
| 7 | 7 | 4 |
| 8 | 11 | 6 |
Tentukan persamaan regresi berdasarkan data tersebut.
Pembahasan:
Perhatikan tabel berikut.
| X | Y | X2 | Y2 | XY |
| 19 | 10 | 361 | 100 | 190 |
| 14 | 8 | 196 | 64 | 112 |
| 14 | 7 | 196 | 49 | 98 |
| 10 | 7 | 100 | 49 | 70 |
| 13 | 8 | 169 | 64 | 104 |
| 16 | 9 | 256 | 81 | 144 |
| 7 | 4 | 49 | 16 | 28 |
| 11 | 6 | 121 | 36 | 66 |
| 104 | 59 | 1448 | 459 | 812 |
Nilai b dan a ditentukan sebagai berikut.
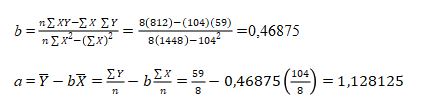
sehingga persamaan regresinya yaitu: Y = 1,128125 + 0,46875X.
Demikian penjelasan mengenai regresi. Semoga bermanfaat.
