Halo Sobat Pintar! Kali ini kita akan membahas contoh soal integral dengan menggunakan sifat-sifat integral tentu dan tak tentu. Tapi sebelum itu, ada baiknya kita refresh dulu materi integral di video berikut yuk!
Gimana sobat? sudah cukup jelas kan? yuk lanjut kita simak soal dan pembahasan berikut untuk meningkatkan pemahamanmu dalam menyelesaikan soal integral.
Contoh Soal Integral
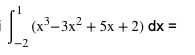
Dalam soal ini, batas atas adalah 1 dan batas bawah -2. Tahap pertama yang perlu kita lakukan adalah melakukan integral fungsi 3x2 + 5x + 2 menjadi seperti di bawah ini.
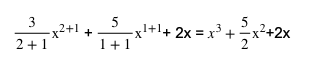
Setelah kita mendapatkan bentuk integral dari fungsi tersebut, kita dapat memasukkan nilai batas atas dan bawah ke dalam fungsi tersebut lalu mengurangkannya menjadi seperti berikut.
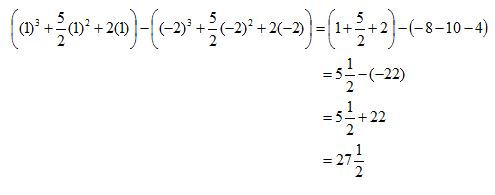
Hasil dari integral tersebut adalah 27,5.
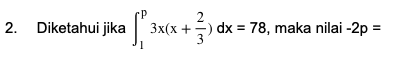
Untuk mengerjakan soal ini, kita dapat mencontoh cara pada soal sebelumnya yaitu melakukan integral fungsi terlebih dahulu kemudian mencari nilai p berdasarkan hasil 78 seperti berikut ini.
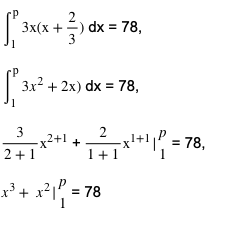
Setelah kita mendapatkan fungsi integral, kita dapat memasukkan batas atas dan bawah ke dalam fungsi tersebut.
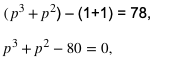
Setelah memasuki fungsi pertidaksamaan tersebut, kita dapat menggunakan sifat pertidaksamaan untuk menyelesaikan soal tersebut sehingga didapatkan nilai P adalah 4. Maka untuk nilai -2p, kita dapat memasukkan nilai 4, maka hasil -2p= -8.
3. Tentukanlah integral x jika f’(x) = 3x2
Dalam mengerjakan soal ini, kita harus memperhatikan fungsi secara seksama. Dalam soal tersebut fungsi berbentuk f’(x) yang menandakan bahwa fungsi tersebut merupakan suatu turunan dari fungsi tertentu. Untuk mengerjakan soal tersebut, kita dapat menggunakan sifat dasar integral tak tentu seperti di bawah.
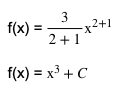
Sehingga nilai integral dari fungsi tersebut adalah x3+C
4. Tentukanlah integral x jika diketahui g’(x) = 3x5+3
Untuk mengerjakan soal ini, kita dapat menggunakan sifat seperti soal pertama. Dalam soal ini, g’(x) merupakan turunan dari suatu fungsi. Berikut ini cara penyelesaiannya
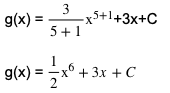
Nilai integral dari g’(x) adalah g(x) = (1/2)x6 + 3x + C
Di atas adalah contoh soal & pembahasan integral sederhana. Untuk kumpulan soal integral lainnya, lanjut di contoh soal berikutnya ya!
Contoh Soal Integral Tentu
Integral tentu merupakan hasil jumlahan suatu daerah yang dibatasi kurva dari suatu persamaan tertentu.
Bedanya dengan integral tak tentu, integral tentu sudah mempunyai nilai pasti karena batas yang ditentukan sudah jelas.
Untuk lebih lengkapnya, silakan baca di Integral Tentu.
Di bawah ini ada beberapa latihan atau contoh soal integral tentu beserta pembahasannya yang sudah kami kumpulkan. Yuk, langsung simak pembahasannya di berikut:
1. Carilah hasil dari ʃ21 6x2 dx !
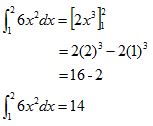
Jadi, hasil dari ʃ21 6x2 dx adalah 14.
2. Tentukan hasil integral tentu dari ʃ-1-4 7 dx !
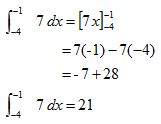
Jadi, hasil integral tentu dari ʃ-1-4 7 dx adalah 21.
3. Berapakah nilai integral tentu dari ʃ-2-2 3x2 – 2x + 1 dx ?
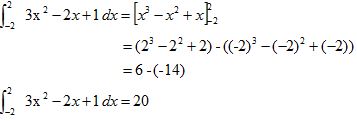
Jadi, nilai integral tentu dari ʃ-2-2 3x2 – 2x + 1 dx adalah 20.
4. Hitunglah nilai integral tentu dari ʃ94 1/√x dx !
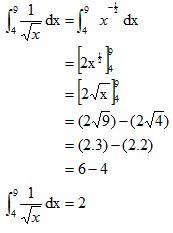
Jadi, nilai integral tentu dari ʃ94 1/√x dx adalah 2.
5. Carilah hasil integral tentu dari ʃπ/3π/6 cos x dx
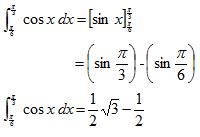
Jadi, hasil integral tentu dari ʃπ/3π/6 cos x dx adalah ½ √3 – ½.
6. Tentukan hasil integral tentu dari ʃπ/20 cos x + sin x dx
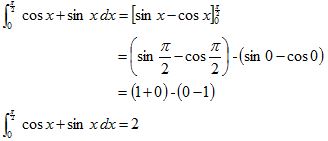
Jadi, hasil integral tentu dari ʃπ/20 cos x + sin xdx adalah 2.
7. Diketahui ʃp1 2x – 4 dx = -1, berapakah nilai 7p?
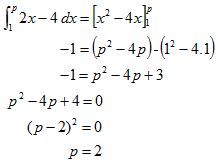
Jadi nilai dari 7p adalah 14.
Contoh Soal Integral Tak Tentu
Integral tak tentu adalah kebalikan dari turunan, atau lebih sering dikenal dengan sebutan anti turunan atau antiderivative.
Hasil dari Integral tak tentu suatu fungsi merupakan suatu fungsi baru yang belum memiliki nilai yang tentu atau pasti karena masih ada variabel dalam fungsi baru tersebut. Untuk lebih lengkapnya, silakan baca di Integral Tak Tentu.
Berikut kami kumpulkan beberapa contoh soal integral tak tentu beserta pembahasannya. Langsung saja simak pembahasannya di bawah ini:
1. Tentukan hasil dari ʃ 3x2 dx !
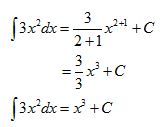
Jadi, hasil dari ʃ 3x2 dx adalah x3 + C.
2. Carilah hasil integral tak tentu dari ʃ 8x3 – 6x2 + 4x – 2 dx.
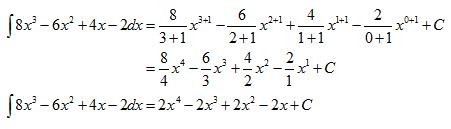
Jadi hasil dari ʃ 8x3 – 6x2 + 4x – 2 dx adalah 2x4 – 2x3 + 2x2 – 2x + C.
3. Tentukan nilai dari ʃ 4 sin x + 7 cos x dx !
ʃ sin x dx = – cos x + C
ʃ cos x dx = sin x + C
Maka:
ʃ 4 sin x + 7 cos x dx = – 4cos x + 7sin x + C
Jadi, nilai dari nilai dari ʃ 4 sin x + 7 cos x dx adalah – 4cos x + 7sin x + C.
4. Carilah nilai dari ʃ (3x-2)(x+6) dx
(3x-2)(x+6) = 3x2 + 18x – 2x -12 = 3x2 + 16x -12
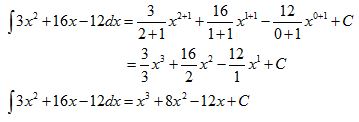
Jadi, hasil dari ʃ (3x-2)(x+6) dx adalah x3 + 8x2 – 12x + C.
5. Hitunglah nilai dari ʃ dx/(3x2) !
ʃ dx/(3x2) = ʃ ⅓ x–2 dx
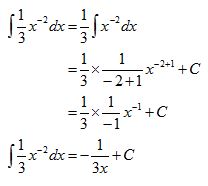
Jadi, nilai dari ʃ dx/(3x2) adalah – 1/(3x) + C.
6. Carilah nilai dari ʃ -5 sin x + 3 cos x – 4 dx!
Ingat!
ʃ sin x dx = – cos x + C
ʃ cos x dx = sin x + C
Maka:
ʃ -5 sin x + 3 cos x – 4 dx = (-5) ( -cos x) + 3 (sin x) – 4 + C
ʃ -5 sin x + 3 cos x – 4 dx = 5 cos x + 3 sin x – 4 + C
Jadi, nilai dari ʃ -5 sin x + 3 cos x – 4 dx adalah 5 cos x + 3 sin x – 4 + C.
7. Tentukan nilai dari ʃ (4x+3)7 dx
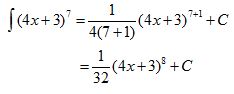
Jadi nilai dari ʃ (4x+3)7 dx adalah 1/32 (4x+3)8 + C
Contoh Soal Integral Parsial
Pada umumnya, Integral parsial digunakan untuk menyelesaikan persoalan integral dari perkalian dua fungsi. Biasanya, rumus integral parsial digunakan jika rumus integral dasar tidak bisa digunakan untuk menyelesaikan persoalan integral.
Untuk lebih lengkapnya, silakan baca di Integral Parsial.
Berikut ini telah kami rangkum beberapa contoh soal integral parsial beserta jawaban dan pembahasannya. Silakan anda simak dan pelajari pembahasannya di bawah ini:
1. Tentukan hasil dari ʃ (2x+1) cos (x + π) dx !
Misal
u = 2x+1
dv = cos (x + π) dx
Maka
du = 2 dx
v = ʃ cos (x + π) dx = sin (x + π)
Sehingga
∫ u dv = uv − ∫v du
∫ u dv = (2x+1) . sin (x +π) − ∫ sin (x + π) . 2 dx
∫ u dv = (2x+1) . sin (x +π) − 2 (− cos (x + π)) + C
∫ u dv = (2x+1) . sin (x +π) + 2 cos (x + π) + C
Jadi, hasil dari ʃ (2x+1) cos (x + π) dx adalah (2x+1) . sin (x +π) + 2 cos (x + π) + C.
2. Berapakah hasil dari ∫ (3x + 2) sin (3x + 2) dx
Misal
u = 3x + 2
dv = sin (3x + 2) dx
Maka
du = 3 dx
v = ʃ sin (3x + 2) dx = − ⅓ cos (3x + 2)
Sehingga
∫ u dv = uv − ∫v du
∫ u dv = (3x + 2) . (− ⅓ cos (3x + 2)) − ∫ (− ⅓ cos (3x + 2)) . 3 dx
∫ u dv = − (x+2/3) . cos (3x + 2) + ⅓ . ⅓ sin (3x + 2) + C
∫ u dv = − (x+2/3) . cos (3x + 2) + 1/9 sin (3x + 2) + C
Jadi, hasil dari ∫ (3x + 2) sin (3x + 2) dx adalah − (x+2/3) . cos (3x + 2) + 1/9 sin (3x + 2) + C.
3. Hitunglah hasil dari ∫ x sin x dx = …
Misal
u = x
dv = sin x dx
Maka
du = 1 dx
v = ʃ sin x dx = − cos x
Sehingga
∫ u dv = uv − ∫v du
∫ u dv = x . ( − cos x) − ∫(− cos x) dx
∫ u dv = − x cos x + sin x + C
Jadi, hasil dari ∫ x sin x dx adalah − x cos x + sin x + C.
4. Carilah hasil dari ∫ x(x + 5)4 dx !
Misal
u = x
dv = (x + 5)4 dx
Maka
du = 1 dx
v = ʃ (x + 5)4 dx = 1/5 (x + 5)5 dx
Sehingga
∫ u dv = uv − ∫v du
∫ u dv = x . ( 1/5 (x + 5)5) − ∫(1/5 (x + 5)5) dx
∫ u dv = x/5 (x + 5)5 − 1/30 (x + 5)6 + C (sampai sini sudah selesai, namun masih bisa disederhanakan)
Penyederhanaan
∫ u dv = x/5 (x + 5)5 − 1/30 (x + 5)6 + C
∫ u dv = x/5 (x + 5)5 − 1/30 (x + 5)(x + 5)5 + C
∫ u dv = (x/5 − 1/30 (x + 5))(x + 5)5 + C
∫ u dv = (6x/30 − x/30 + 5/30))(x + 5)5 + C
∫ u dv = (5x/30 + 5/30))(x + 5)5 + C
∫ u dv = 5/30(x + 1)(x + 5)5 + C
∫ u dv = 1/6(x + 1)(x + 5)5 + C
Jadi, hasil dari ∫ x(x + 5)4 dx adalah 1/6(x + 1)(x + 5)5 + C
5. Tentukan hasil dari ∫ (x2 + 1) sin x dx !
Misal
u = x2 + 1
dv = sin x dx
Maka
du = 2x dx
v = ʃ sin x dx = – cos x
Diperoleh
∫ u dv = uv − ∫v du
∫ u dv = (x2 + 1)(- cos x) – ʃ (- cos x) 2x dx
∫ u dv = – (x2 + 1) cos x + ʃ 2x cos x dx … (1)
Karena ʃ 2x cos x dx tidak bisa langsung diintegralkan, maka kita harus mengulangi proses integral parsial untuk menemukan hasil ʃ 2x cos x dx terlebih dahulu.
Agar tidak sama dengan permisalan sebelumnya, kita gunakan variabel lain
Misal
a = 2x
db = cos x dx
Maka
da = 2 dx
b = ʃ cos x dx = sin x
Diperoleh
∫ a db = ab − ∫b da
∫ a db = 2x sin x − ∫ sin x . 2 dx
∫ a db = 2x sin x − 2 (-cos x)
∫ a db = 2x sin x + 2 cos x + C
ʃ 2x cos x dx = 2x sin x + 2 cos x
Selanjutnya, substitusikan hasil ʃ 2x cos x dx ke (1), sehingga diperoleh
∫ u dv = – (x2 + 1) cos x + ʃ 2x cos x dx
∫ u dv = – (x2 + 1) cos x +2x sin x + 2 cos x + C
∫ u dv = – x2 cos x – cos x +2x sin x + 2 cos x + C
∫ u dv = – x2 cos x + cos x +2x sin x + C
∫ u dv = (1 – x2) cos x +2x sin x + C
Jadi, hasil dari ∫ (x2 + 1) sin x dx adalah (1 – x2) cos x +2x sin x + C.
Demikian beberapa latihan soal integral tentu, integral tak tentu, integral parsial beserta pembahasannya. Semoga dengan latihan soal di atas bisa bermanfaat untuk meningkatkan kemampuan dalam menyelesaikan soal-soal integral.
Sekian dari rumuspintar, selamat belajar.
