Dibandingkan dengan istilah lain di dalam ilmu ekonomi, anuitas mungkin adalah salah satu istilah yang tidak populer. Hanya orang yang pernah bersinggungan dengan dunia perbankan yang tahu istilah anuitas.
Walau demikian, orang-orang itu pun mungkin juga tidak terlalu paham artinya, sebab biasanya perihal anuitas hanya diberikan sebagai pelengkap informasi saja. Padahal tidak ada salahnya untuk memahami salah satu komponen dalam dunia perbankan ini.
Pengertian Anuitas
Pengertian dari anuitas adalah pembayaran yang dilakukan dalam periode tertentu dengan besaran yang sama secara berkala dan konstan. Orang awam mungkin akan lebih akrab jika dimunculkan kata cicilan, walaupun sebenarnya artinya sedikit berbeda dari anuitas.
Jika cicilan lebih dekat dengan dunia kredit, anuitas lebih ke arah debit. Misalnya untuk pembayaran hipotek atau premi asuransi. Dengan adanya anuitas, maka nasabah bisa lebih gampang dalam melakukan transaksi dan mendapatkan keuntungan.
Jenis Anuitas
1. Ordinary Annuity
Jenis ini juga disebut sebagai anuitas biasa yang sering kita kenal dalam kehidupan sehari-hari. Besarnya pembayaran yang dilakukan nasabah dilakukan di akhir periode waktu tertentu. Contoh yang paling mudah adalah membayar hipotek.
2. Due Annuity
Berbeda dengan ordinary annuity yang proses pembayarannya terjadi di akhir periode, due annuity atau anuitas tempo, pembayaran dilakukan di awal periode. Misalnya pembayaran sewa hingga setoran tunai untuk tabungan.
3. Deferred Annuity
Yang dimaksud dengan anuitas tangguhan atau deferred annuity adalah metode anuitas yang pembayarannya dilakukan setelah sudah berjalan selama beberapa periode. Itulah sebabnya penerimaannya ditahan. Contoh sederhana dan sering kita lihat adalah pembayaran bunga deposito.
4. Immediate Annuity
Sesuai dengan namanya, maka pembayaran dilakukan secara langsung. Misalnya adalah pembayaran untuk kredit mobil.
Rumus Anuitas
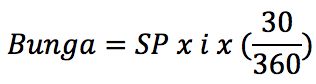
Keterangan:
- SP adalah saldo pokok pinjaman di bulan sebelumnya.
- i adalah suku bunga per tahun.
- 30 adalah jumlah hari dalam satu (1) bulan.
- 360 adalah jumlah hari dalam satu (1) tahun.
Namun, rumus ini masih dikembangkan lagi hingga menjadi seperti berikut:
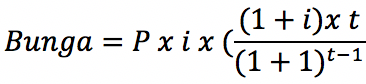
Keterangan:
- P adalah pokok pinjaman.
- i adalah suku bunga.
- t adalah periode kredit.
Tabel Anuitas
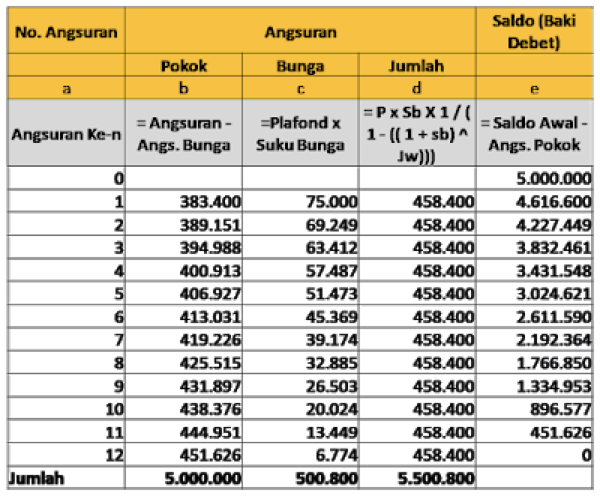
Bunga Anuitas
Modifikasi dari bunga efektif adalah gambaran yang paling dekat untuk menjabarkan arti dari bunga anuitas. Prinsip kedua bunga tersebut sama, yaitu memakai perhitungan bunga yang adil.
Adil yang dimaksud adalah perhitungan bunga diambil dari sisa pokok yang masih terhutang. Sedangkan yang membedakan antara keduanya adalah jumlah cicilan tiap bulan.
Cicilan pada bunga efektif biasanya cenderung menurun setiap periode bayarnya, sedangkan cicilan bunga anuitas diusahakan selalu tetap. Maka dari itulah, bunga anuitas sering digunakan untuk perhitungan Kredit Pemilikan Rumah maupun kredit jangka panjang lainnya.
Misal:
P = pokok pinjaman
i = suku bunga per tahun
t = lama kredit dalam bulan
Maka:
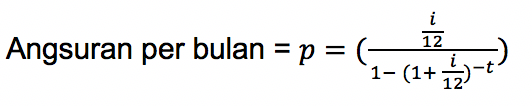
Contoh Soal Anuitas
Marzuki memiliki utang sebesar 6 juta. Proses pelunasan utang akan menggunakan metode bunga anuitas dengan besaran 1 juta dengan suku bunga 2% per bulan. Maka hitung:
a. Perhitungan angsuran
b. Tabel rencana angsuran
Diketahui:
M = 6.000.000 atau 6 x 106
b = 2% = 0.02
A= anuitas = 1.000.000
Misalkan:
an = angsuran pada bulan ke-n
bn = bunga pada akhir bulan ke-n
Mn = sisa utang pada bulan ke-n ; dengan n = 1,2,3,…
Jawaban a
Proses perhitungan angsuran (an) berdasarkan aturan
Angsuran pertama (ai) = anuitas – bunga akhir bulan ke-i (secara formula: an = A – bn)
- Angsuran pertama (a1)
M1 (Utang bulan ke-1) = 6 x 106
B1 (Bunga akhir bulan ke-1) = 0,02 x 6 x 106 = 105
A1 (Angsuran ke-1) = A – b1
= 1.000.000 – 100.000 = 900.000
- Angsuran kedua (a2)
M2 (Utang pada bulan ke-2) = M1 – a1
= 6 x 106 – 900.000
= 5.100.000
B2 (Bunga pada akhir bulan ke-2) = 0,02 x 5.100.000
= 102.000
A2 (Angsuran ke-2) = A – b2
= 1.000.000 – 102.000
= 898.000
- Angsuran ketiga (a3)
M3 (Utang pada bulan ke-3) = M2 – a2
= 5.100.000 – 898.000
= 4.202.000
B3 (Bunga pada akhir bulan ke-3) = 0,02 x 4.202.000
= 84.040
A3 (Angsuran ke-3)= A – b3
= 1.000.000 – 84.040
= 915.960
- Angsuran keempat (a4)
M4 (Utang pada bulan ke-4) = M3 – a3
= 4.202.000 – 915.960
= 3.286.040
B4 (Bunga pada akhir bulan ke-4) = 0,02 x 3.286.040
= 65.720,8
A4 (Angsuran ke-4) = A – b4
= 1.000.000 – 65.720,8
= 934.279,2
- Angsuran kelima (a5)
M5 (Utang pada bulan ke-5)= M4 – a4
= 3.286.040 – 934.279,2
= 2.351.760,8
B5 (Bunga pada akhir bulan ke-5) = 0,02 x 2.351.760,8
= 47.035,216
A5 (Angsuran ke-5) = A – b5
= 1.000.000 – 47.035,216
= 952.964,784
- Angsuran keenam (a6)
M6 (Utang pada bulan ke-6)= M5 – a5
= 2.351.760,8 – 952.964,784
= 1.398.769,02
B6 (Bunga pada akhir bulan ke-6) = 0,02 x 1.398.769,02
= 27.975,3804
A6 (Angsuran ke-6) = A – b6
= 1.000.000 – 27.975,3804
= 972.024,62
- Angsuran ketujuh (a7)
M7 (Utang pada bulan ke-7)= M6 – a6
= 1.398.769,02 – 972.024,62
= 426.744,4
B7 (Bunga pada akhir bulan ke-7) = 0,02 x 426.744,4
= 8.534,888
A7 (Angsuran ke-7)= A – b6
= 1.000.000 – 8.534,888
= 991.465,112
Berdasarkan penyelesaian di atas, maka utang Marzuki akan lunas dalam waktu 7 bulan. Seperti yang sudah disampaikan di awal, tidak ada salahnya mempelajari tentang anuitas ini. Dari penjelasan di atas, sudah sangat gamblang dan jelas pembahasan tentang anuitas, bukan? Jika berkecimpung di dunia perbankan, pasti penjelasan di atas sangat bermanfaat.
