Berikut ini merupakan pembahasan materi dengan topik dimensi tiga.
Dalam matematika, khususnya geometri, terdapat topik mengenai bangun datar dan bangun ruang.
Lalu ada yang membedakan keduanya?
Bangun datar dan bangun ruang dibedakan berdasarkan dimensinya. Bangun datar merupakan bangun berbentuk dua dimensi, sedangkan bangun ruang merupakan bangun tiga dimensi.
Contoh-contoh bangun ruang tiga dimensi yaitu kubus, balok, prisma, limas, kerucut, tabung, dan bola.
Dalam konsep dimensi tiga terdapat beberapa istilah seperti jarak antar titik, jarak antar garis, dan sebagainya.
Untuk lebih jelasnya, simak penjelasan mengenai dimensi tiga berikut.
Pengertian Dimensi 3
Dimensi 3 merupakan salah satu materi yang dipelajari di tingkat sekolah. Dimensi 3 adalah suatu objek yang mempunyai ruang.
Dalam dimensi 3 dipelajari beberapa konsep seperti kedudukan titik, kedudukan garis, dan kedudukan bidang dari suatu bangun 3 dimensi.
Sebelum mempelajari dimensi 3, pemahaman mengenai diagonal bidang dan diagonal ruang diperlukan untuk mempelajari konsep dimensi 3.
Berikut ini akan dijelaskan beberapa contoh penerapan dimensi 3.
Contoh Penerapan Dimensi 3
Dimensi 3 mencangkup konsep mengenai kedudukan (titik, garis, bidang), jarak antar titik, dan sebagainya.
Oleh karena itu konsep dimensi 3 ini dapat diterapkan untuk menyelesaikan permasalahan berkaitan dengan kedudukan titik, kedudukan garis, kedudukan bidang, jarak antar titik, dan sebagainya.
Beberapa konsep yang dipelajari dalam dimensi 3 dijelaskan pada bagian berikut.
Perhatikan gambar salah satu bangun dimensi 3 berikut.
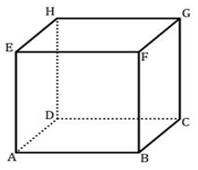
Kedudukan Suatu Titik
Kedudukan suatu titik dibedakan menjadi dua, yaitu kedudukan titik terhadap garis dan kedudukan titik terhadap bidang.
Kedudukan titik terhadap garis dibagi menjadi 3 macam, yaitu kedudukan titik pada garis, kedudukan titik pada perpanjangan garis, dan kedudukan titik di luar garis.
Berdasarkan gambar di atas, beberapa contoh kedudukan titik yaitu titik A pada garis AB (titik pada garis) dan titik B terhadap garis AE (di luar garis).
Kedudukan Garis
Kedudukan garis juga dibedakan menjadi dua, yaitu kedudukan garis terhadap garis dan kedudukan garis terhadap bidang. Kedudukan garis terhadap garis pada dimensi 3 dibagi menjadi 4, yaitu:
Dua Garis Sejajar
Dua garis dikatakan sejajar apabila kedua garis tersebut mempunyai jarak yang sama di setiap titiknya dan kedua garis tidak mempunyai titik potong.
Berdasarkan gambar di atas, contohnya yaitu garis AB sejajar dengan garis DC, garis AE sejajar dengan garis BF, dan lainnya.
Dua Garis Berhimpitan
Dua garis berhimpitan apabila posisi setiap titik dari kedua garis tersebut berhimpitan atau letaknya sama.
Dua Garis Berpotongan
Dua garis dapat disebut berpotongan apabila kedua garis tersebut memiliki titik potong. Berdasarkan gambar di atas, contohnya yaitu garis AB dan AD memiliki perpotongan di titik A.
Dua Garis Bersilangan
Dua garis bersilangan tidak mempunyai titik potong karena terletak pada bidang yang berbeda. Berdasarkan gambar di atas, contohnya yaitu garis AB dengan garis CG.
Kedudukan garis terhadap bidang dibedakan menjadi 3 yaitu, garis yang terletak pada bidang, garis yang berpotongan dengan bidang, dan garis yang sejajar dengan bidang.
Beberapa contoh kedudukan garis sesuai dengan gambar di atas yaitu garis AB terhadap bidang ABCD (garis pada bidang), garis BF dengan bidang ABCD (berpotongan di titik B), dan garis EF dengan bidang ABCD (sejajar dengan bidang).
Kedudukan Bidang
Kedudukan bidang dengan bidang lainnya dibagi menjadi 3 yaitu dua bidang yang sejajar, dua bidang yang berpotongan dan dua bidang yang berhimpitan.
Contoh berdasarkan gambar di atas yaitu, bidang ABCD dengan bidang EFGH (sejajar), bidang ABCD dengan bidang ABFE (berpotongan pada garis AB), dan bidang ABCD dengan bidang ABD (berhimpitan).
Berikut ini akan dijelaskan rumus mengenai jarak pada dimensi 3.
Perhatikan kembali gambar berikut.

Jarak titik ke titik
Berdasarkan bangun di atas, misalnya akan ditentukan jarak titik A ke titik F, maka:
AF2 = AB2 + BF2
AF = √( AB2 + BF2)
Jarak Titik ke Garis
Misalnya akan ditentukan jarak titik B terhadap garis CE. Langkah pertama yang dilakukan adalah menentukan panjang CE, BE, dan BC.
Kemudian dengan menerapkan kesamaan luas segitiga BCE dapat ditentukan jarak titik B terhadap garis CE. Cara lainnya yaitu dengan menggunakan teorema Pythagoras.
Demikian penjelasan mengenai dimensi 3. Semoga penjelasan di atas dapat menambah pemahaman kalian mengenai dimensi 3. Terima kasih.
