Pengertian Kerucut
Secara umum, kerucut merupakan sebuah bangun ruang yang memiliki satu buah titik sudut dan dua buah sisi.
Salah satu sisinya adalah alas kerucut yang berbentuk lingkaran, dan sisi yang lain merupakan selimut bangun kerucut.
Di bawah ini merupakan gambar bangun kerucut beserta keterangannya:
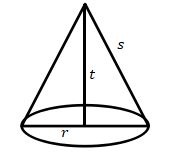
Keterangan:
r: jari-jari alas kerucut
s: garis pelukis kerucut
t: tinggi kerucut
Benda-benda dalam kehidupan sehari-hari dengan bentuk seperti pada gambar di atas antara lain nasi tumpeng, topi ulang tahun, dan caping.
Jaring-jaring kerucut
Pada dasarnya, setiap bangun ruang memiliki jaring-jaring atau kerangka penyusunnya yang berupa bidang. Begitu pula pada bangun ruang kerucut yang memiliki jaring-jaring dengan jumlah bidang sebanyak dua buah seperti pada Gambar.1 dibawah ini:
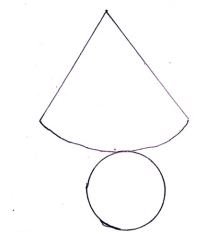
Irisan kerucut
Selain kerangka atau jaring-jaring kerucut, terdapat pula sebuah istilah yang disebut “irisan kerucut”.
Irisan kerucut adalah lokus dari semua titik yang membentuk kurva dua dimensi dan terbentuk oleh irisan sebuah kerucut dengan sebuah bidang datar.
Irisan kerucut memiliki 4 (empat) jenis, yaitu:
1. Parabola
Irisan dengan bentuk parabola akan didapatkan apabila bidang datar memotong satu kerucut (Gambar.2 poin a)
2. Hiperbola
Irisan dengan bentuk hiperbola akan didapatkan apabila bidang datar memotong dua kerucut (Gambar.2 poin b)
3. Elips
Irisan dengan bentuk elips akan didapatkan apabila bidang datar memotong satu kerucut secara tidak tegak lurus dengan garis sumbu utama (Gambar.2 poin c)
4. Lingkaran
Irisan dengan bentuk lingkaran akan didapatkan apabila bidang datar memotong satu kerucut secara tegak lurus dengan garis sumbu utama (Gambar.2 poin d)
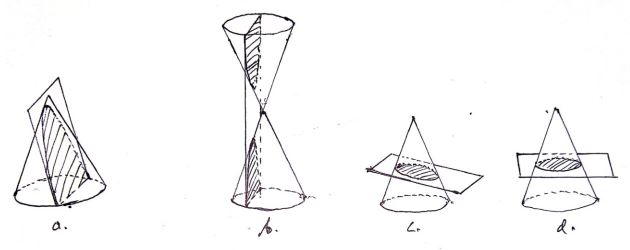
Dari gambar di atas, dapat diketahui bagaimana sebuah bidang memotong kerucut dan membentuk sebuah irisan kerucut.
Rumus kerucut
Setelah kita mengetahui apa itu kerucut dan bagaimana bentuk, kerangka, serta irisannya, sekarang kita akan mengetahui bahwa kerucut adalah sebuah bangun ruang.
Karenanya, kerucut pasti memiliki volume. Volume dari sebuah kerucut dapat dihitung dengan mengalikan luas alas kerucut (luas lingkaran) dengan tinggi kerucut yang dirumuskan seperti di bawah ini:
V = ⅓ × πr2 × t
dengan
- V = Volume Kerucut

- r = jari – jari alas
- t = tinggi kerucut
Selain volume, kerucut juga memiliki permukaan yang dapat dihitung pula luasnya. Rumus luas permukaan kerucut adalah sebagai berikut:
L = πr2 + πrs
dengan
- L = Luas Permukaan Kerucut
- s = Garis Pelukis Kerucut
Selanjutnya akan diberikan contoh soal tentang menghitung volume dan luas permukaan kerucut.
Contoh soal Kerucut
Nisa genap berumur 20 tahun pada akhir Mei tahun ini. Karena itu, Nisa mengadakan acara syukuran yang diadakan di rumahnya. Pada acara syukuran tersebut, terdapat sebuah nasi tumpeng berbentuk kerucut yang memiliki tinggi 24 cm dan diameter 20 cm. Hitunglah volume dan luas permukaan nasi tumpeng tersebut.
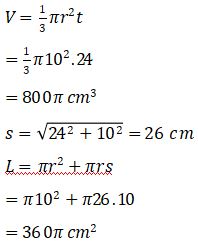
Jadi, volume nasi tumpeng tersebut adalah 800π cm3 dan luas permukaannya adalah 360π cm3.
Cara cepat menghitung volume dan luas permukaan kerucut
Dalam penghitungan volume kerucut, tidak ada rumus cepat yang dapat dilakukan. Namun perlu dipahami bahwa setiap bangun ruang yang serupa dengan limas memiliki rumus volume yang sama, yaitu:
V = ⅓ × Luas alas × Tinggi Kerucut
Cara penghitungan tersebut akan menjadi sangat efisien sehingga menghemat waktu dengan catatan sudah pengguna rumus cepat sudah menghafal rumus menghitung luas bangun datar.
Kemudian untuk penghitungan luas permukaan kerucut, rumus awal dapat disederhanakan menggunakan proses aljabar menjadi:
L = π r (r + s)
Contoh soal
Sebuah topi ulang tahun berbentuk kerucut memiliki diameter, tinggi, dan garis pelukis. Hitung volume dan luas permukaan topi ulang tahun tersebut!
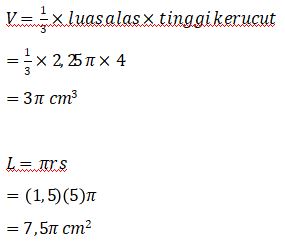
Jadi, volume topi ulang tahun adalah 3π cm3 dan luas permukaannya sama dengan luas selimut karena berlubang (tidak ada alasnya) yaitu 7,5π cm2.
