Kubus: Pengertian, Jaring, Luas & Volume, Contoh Soal

Pada artikel kali ini kita akan belajar mengenai salah satu bangun ruang, yaitu kubus.

Kita menjumpai banyak benda dalam kegiatan sehari-hari. Ada benda yang berbentuk dua dimensi maupun tiga dimensi.

Ada banyak sekali benda-benda tiga dimensi dalam berbagai bentuk. Terdapat benda yang bentuknya menyerupai kubus dengan sisi-sisinya berbentuk persegi.

Pada materi kali ini akan dibahas mengenai bangun ruang kubus, tetapi sebaiknya kalian mengingat materi mengenai bangun persegi.

Jika kalian masih mengingatnya, langsung simak materi berikut ini.

Pengertian Kubus

Perhatikan gambar bangun ruang berikut.

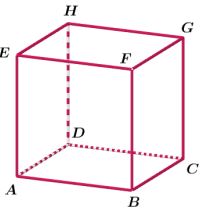
Bangun ruang tersebut merupakan bangun ruang kubus. Kubus adalah bangun ruang yang dibatasi oleh enam sisi yang berbentuk persegi.

Dari gambar di atas, dapatkah kalian menyebutkan ciri-ciri kubus?

Kubus mempunyai enam sisi yang berukuran sama (kongruen), mempunyai delapan titik sudut, dan dua belas rusuk yang sama panjang.

Kubus di atas dapat kita beri nama sebagai kubus ABCD.EFGH. Selanjutnya kita akan belajar mengenai beberapa contoh penerapan kubus.

Kubus dalam Kehidupan Sehari-hari

Benda-benda yang menyerupai kubus banyak kita jumpai. Pernahkah kalian bermain monopoli atau ular tangga?

Dalam permainan tersebut kita menggunakan dadu yang memiliki bentuk menyerupai kubus.

Dadu memiliki enam sisi yang setiap sisinya memiliki mata dadu 1 – 6. Selanjutnya kita akan membahas mengenai rusuk, diagonal ruang, bidang diagonal, dan jaring-jaring kubus.

Rusuk Kubus

Perhatikan kembali kubus pada gambar 1 di atas.

Berapa banyak rusuk pada kubus ABCD.EFGH?

• Pada kubus tersebut terdapat 12 rusuk.
• Rusuk-rusuk pada kubus memiliki ukuran yang sama panjang.
• Rusuk AB sejejar dengan rusuk CD, EF, dan GH.
• Rusuk BC sejajar dengan rusuk AD, EH, dan FG.
• Rusuk AE sejajar dengan rusuk BF, CG, dan DH.

Diagonal Ruang Kubus

Perhatikan gambar berikut.

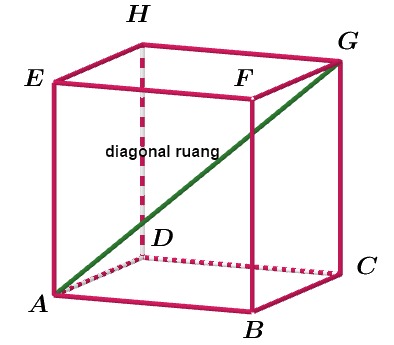
Kubus memiliki empat diagonal ruang yang menghubungkan dua titik sudut yang berhadapan.

Terdapat ruang tersebut antara lain AG, BH, CE, dah DF.

Misalkan panjang rusuk pada kubus tersebut adalah r, maka panjang diagonal ruang kubus yaitu

AC = √(AB² + BC²) = √(r² + r²) = √(2r²) = r √2

AG = √(AC² + CG²) = √((r √2)² + r²) = √(3r²) = r √3

Jadi, panjang diagonal ruang kubus dengan rusuk r adalah r √3.

Bidang Diagonal Kubus

Perhatikan salah satu bidang diagonal kubus berikut.

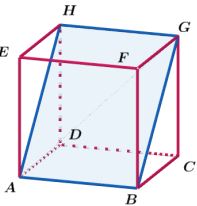
Gambar tersebut merupakan salah satu bidang diagonal kubus, yaitu bidang diagonal ABGH.

Dapatkah kalian menyebutkan bidang diagonal yang lainnya?

Bidang diagonal kubus yang lainnya yaitu bidang diagonal CDEF, ADGF, BCHE, ACGE, dan BFHD. Sehingga terdapat 6 bidang diagonal pada kubus.

Bidang diagonal kubus memiliki luas yang sama. Misalkan ukuran panjang rusuk kubus adalah r, maka luas bidang diagonalnya (misal bidang diagonal ABGH):

Jaring-Jaring Kubus

Terdapat banyak jarin-jaring kubus yang dapat dibuat. Pada artikel kali ini akan disajikan dua contoh jaring-jaring kubus.

Perhatikan jaring-jaring kubus berikut.

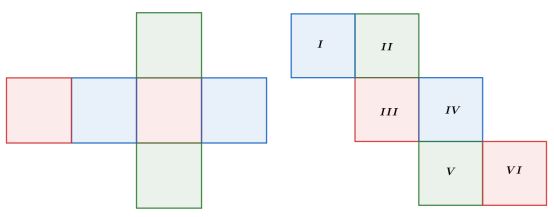
Pada dua jaring-jaring kubus tersebut, bagian yang berwarna sama merupakan sisi-sisi kubus yang saling berhadapan.

Jaring-jaring kubus tersusun dari enam buah persegi yang sama (kongruen).

Pada jaring-jaring kubus kedua terdapat kode dari I sampai VI.

Persegi I berhadapan dengan persegi IV, persegi II berhadapan dengan persegi V, dan persegi III berhadapan dengan persegi VI.

Selanjutnya akan dijelaskan beberapa rumus pada kubus.

Rumus Kubus

Rumus yang akan disampaikan pada bagian ini meliputi rumus luas permukaan kubus dan volume kubus.

Luas Permukaan Kubus

Perhatikan gambar berikut.

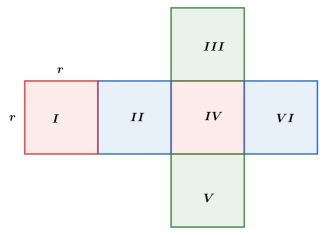
Sebelumnya kita teah membahas mengenai jaring-jaring kubus. Dengan menggunakan jaring-jaring kubus kita dapat menentukan rumus luas permukaan kubus.

Kubus tersusun dari enam sisi yang berbentuk persegi. Misalkan panjang rusuk kubus adalah r, maka luas permukaannya yaitu:

Selanjutnya dijelaskan mengenai volume kubus.

Volume Kubus

Perhatikan gambar berikut

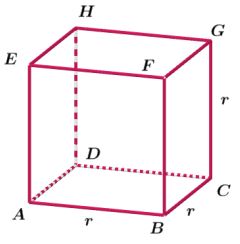
Pada gambar di atas terdapat kubus ABCD.EFGH dengan panjang rusuk r.

Secara umum, volume prisma adalah luas alas dikali dengn tinggi prisma.

Karena alas kubus berbentuk persegi dengan panjang sisi r, maka luas alasnya adalah r².

Kerjakan soal latihan berikut.

Soal dan Pembahasan

Diketahui suatu kubus dengan panjang rusuk 8 cm. Tentukan:

1. Ukuran diagonal ruang kubus,
2. Luas bidang diagonal kubus,
3. Luas permukaan kubus, dan
4. Volume kubus

Mari kita simpulkan materi kubus pada artikel ini. Baca juga Balok.

Kesimpulan

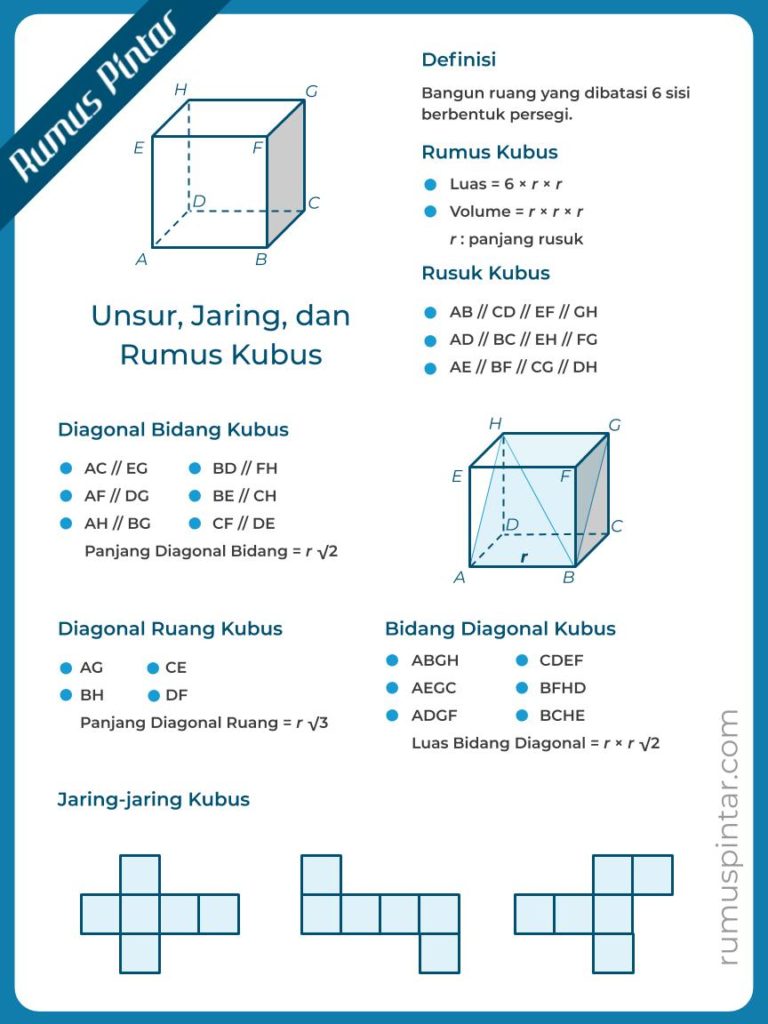
• Kubus adalah bangun ruang yang dibatasi oleh enam sisi yang berbentuk persegi.
• Kubus memiliki 12 rusuk yang ukurannya sama panjang.
• Kubus memiliki empat diagonal ruang yang sama (kongruen).
• Kubus memiliki enam bidang diagonal yang sama (kongruen).
• Kubus memiliki jarin-jaring yang bermacam-macam.

Jika terdapat kubus dengan rusuk r , maka:

• Ukuran diagonal ruangnya adalah r √3
• Luas bidang diagonalnya adalah r² √2
• Luas permukaan kubus adalah 6 x r²
• Voume kubus adalah r³.

Sekian informasi yang dapat disampaikan. Semoga bermanfaat.