Pada artikel kali ini, kita akan membahas mengenai permutasi dan kombinasi.
Apakah kalian sudah mengenal notasi faktorial?
Notasi faktorial dilambangkan dengan tanda “ ! “. Misalkan kita akan menghitung hasil dari 4!. Nilai dari 4! Dapat dihitung sebagai 4 x 3 x 2 x 1 = 24.
Jika kalian sudah memahaminya, kita akan lanjut ke materi berikutnya yaitu mengenai permutasi dan kombinasi.
Definisi Permutasi dan Kombinasi
Permutasi dapat diartikan sebagai aturan pencacahan/penyusunan dengan memperhatikan urutan objek.
Sedangkan kombinasi merupakan suatu aturan pencacahan/penyusunan tanpa memperhatikan urutan objek.
Perhatikan dua permasalahan di bawah ini.
Permasalahan 1
Dalam suatu lomba yang diikuti oleh 10 peserta akan diambil juara 1, juara 2, dan juara 3. Berapa banyaknya kemungkinan susunan pemenang?
Permasalahan 2
Dalam suatu kelas yang terdiri dari 12 siswa akan dikirimkan delegasi yang terdiri dari 3 orang. Berapa banyak susunan delegasi yang mungkin?
Dari dua permasalahan tersebut, dapatkah kalian membedakan manakah permasalahan yang menerapkan konsep permutasi atau kombinasi untuk menyelesaikaanya?
Pada permasalahan pertama, konsep yang digunakan adalah konsep permutasi.
Mengapa menggunakan konsep permutasi?
Karena pada permasalahan tersebut memperhatikan urutan, yaitu juara 1, juara 2, dan juara 3.
Sedangkan pada permasalahan dua kita dapat menyelesaikannya dengan konsep kombinasi karena permasalahan tersebut penyusunannya tidak memperhatikan urutan.
Selanjutnya akan diberikan contoh penerapan permutasi dan kombinasi.
Permutasi dan Kombinasi dalam Kehidupan Sehari-hari
Permutasi dan kombinasi sering kita terapkan pada kehidupan sehari-hari.
Misalkan saat kita menyusun telur dalam suatu tempat. Jika kita memiliki 10 butir telur dan 5 tempat/wadah, berapa banyak susunan berbeda yang mungkin?
Selain itu, konsep permutasi dan kombinasi dapat diterapkan dalam permasalahan mengenai susunan tempat duduk dan lain sebagainya.
Lebih lanjut, dengan menggunakan konsep permutasi dan kombinasi, kalian akan dapat menentukan peluang suatu kejadian untuk memprediksi/memperkirakan kejadian yang mungkin di masa mendatang.
Perbedaan Permutasi dan Kombinasi
Terdapat beberapa perbedaan antara permutasi dan kombinasi. Perbedaan tersebut salah satunya yaitu permutasi memperhatikan urutan objek, sedangkan pada kombinasi tidak memperhatikan urutan.
Akibatnya permutasi dan kombinasi pun memiliki perbedaan dalam penyelesaiannya. Rumus untuk permutasi dan kombinasi akan disajikan dalam bagian di bawah ini.
Rumus Permutasi
Secara umum, rumus permutasi yaitu sebagai berikut.
P(n, r) = n!/(n-r)!
Keterangan:
- P(n, r) : permutasi r objek dari n objek yang ada
- n : banyaknya objek keseluruhan
- r : banyaknya objek yang diamati/diberi perlakuan
Yuk simak penjelasan lebih lengkap di video rumus pintar berikut.
Salah satu macam permutasi yang perlu kalian ketahui adalah permutasi siklis. Penjelasan mengenai permutasi siklis akan disampaikan pada bagian di bawah ini.
Permutasi Siklis
Pembahasan mengenai permutasi siklis penting untuk dipelajari. Coba pahami permasalahan berikut ini.
Dalam suatu restoran, terdapat 6 orang yang duduk secara melingkar. Berapa banyak susunan tempat duduk yang mungkin?
Apakah kalian akan menyelesaikan permasalahan tersebut menggunakan rumus permutasi pada pembahasan sebelumnya?
Coba kalian amati gambar berikut.
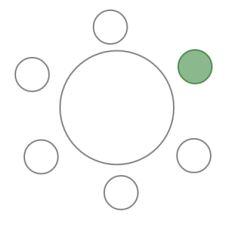
Untuk menentukan banyaknya susunan tempat duduk berbeda untuk 6 orang yang duduk melingkar dapat kita mulai dengan menentukan salah satu tempat duduk sebagai acuan. Sehingga tersisa 5 tempat duduk yang lainnya.
Dari 5 tempat duduk tersebut, jika kita mencoba menentukan banyaknya susunan yaitu:
- Kursi 1 : banyaknya kemungkinan orang yang duduk pada kursi tersebut ada 5
- Kursi 2 : banyaknya kemungkinan orang yang duduk pada kursi tersebut ada 4
- Kursi 3 : banyaknya kemungkinan orang yang duduk pada kursi tersebut ada 3
- Kursi 4 : banyaknya kemungkinan orang yang duduk pada kursi tersebut ada 2
- Kursi 5 : banyaknya kemungkinan orang yang duduk pada kursi tersebut ada 1
Dengan menerapkan konsep aturan perkalian diperoleh
Banyaknya susunan duduk = 5 x 4 x 3 x 2 x 1 = 120 cara.
Sehingga, secara umum, rumus permutasi siklik untuk n objek yaitu:
Psiklik(n) = (n – 1)!
Keterangan:
- Psiklik(n) : banyaknya permutasi siklik dari n objek
- n : banyaknya objek
Selain permutasi siklis, ada juga permutasi khusus lainnya. Untuk penjelasannya bisa disimak di video rumus pintar berikut ya.
Selanjutnya, coba kerjakan latihan soal permutasi berikut.
Contoh Soal Permutasi
1. Perusahaan pengalengan sedang membutuhkan 4 karyawan baru untuk mengisi posisi berbeda yang kosong. Namun, calon yang tersedia sebanyak 9. Tentukan berapa banyak susunan karyawan yang mungkin dilakukan.
Dalam mengerjakan sebuah soal permutasi, kita harus mengetahui jenis-jenis rumus permutasi dengan prasyaratnya.
Dalam soal di atas, 4 merupakan bagian di atas, sehingga kita dapat menggunakan persamaan permutasi anggota bagian.
Untuk lebih jelasnya, dapat melihat penyelesaian di bawah ini.
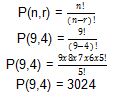
Dalam memilih susunan karyawan yang diterima terdapat 3024 cara.
2. Seorang ilmuwan ingin menyusun kata dari 8 huruf. Tentukan berapa banyak susunan 5 huruf yang bisa dibuat oleh ilmuwan tersebut!
Sama seperti soal di atas, kita harus mengetahui jenis permutasi yang kita kerjakan apakah termasuk anggota himpunan, siklis, atau perulangan.
Dalam soal di atas, ilmuwan ingin membuat susunan 5 huruf dari 9 huruf sehingga 5 adalah bagian dari 8.
Sehingga kita dapat menuliskan penyelesaian permutasinya seperti di bawah.
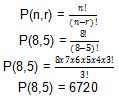
Kita dapat membuat sebanyak 6720 susunan 5 huruf dari 8 huruf yang ada.
3. Terdapat 8 orang yang sedang bermain bersama. Dalam permainan tersebut, disediakan 4 kursi kosong dan 1 kursi telah terisi. Berapakah banyak susunan yang bisa di buat dari sisi anak yang belum duduk?
Berdasarkan informasi soal di atas, terdapat 8 orang yang memperebutkan 4 kursi kosong.
Namun, 1 orang telah menduduki kursi sehingga terdapat 7 orang yang memperebutkan 3 kursi kosong.
Dalam membuat susunan 7 orang, kita dapat menggunakan permutasi anggota himpunan dikarenakan 3 bagian dari 7.
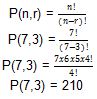
Untuk membuat susunan 3 kursi kosong dengan sisa 7 orang adalah 210 cara.
4. Desa Mawar berencana untuk mengadakan kegiatan HUT RI dengan membuat 3 panitia inti yang terdiri dari ketua, sekretaris, bendahara. Jika calon panitia ada 8 orang, maka berapakah susunan panitia inti yang dapat di buat?
Seperti soal sebelumnya, kita perlu memperhatikan jenis permutasi yang terjadi. Pada soal tersebut, 3 merupakan bagian dari 8 sehingga dapat menggunakan permutasi anggota bagian. Untuk pengerjaannya sama seperti soal sebelumnya.
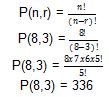
Untuk membuat banyak susunan panitia yang terdiri dari 3 orang panitia inti adalah 336 cara.
5. Jika ada 6 orang sedang mengelilingi meja bundar, ada berapa banyak cara yang dilakukan untuk mendapatkan urutan duduk yang berbeda?
Dalam menyelesaikan soal di atas, kita perlu meninjau permutasi yang di terapkan.
Dalam soal tersebut, dilakukan penyusunan secara memutar dari 6 orang. Sehingga dalam menyelesaikan soal ini, kita dapat menggunakan permutasi siklis.
Untuk lebih jelasnya, dapat melihat penyelesaian di bawah ini.
nPsiklis = (n-1)!
nPsiklis = (6-1)!
nPsiklis = 5!
nPsiklis = 5x4x3x2x1 = 120
Penyusunan yang bisa dilakukan pada 6 orang yang memutar dengan urutan yang berbeda adalah 120 susunan.
6. Dalam suatu pemilihan pengurus kelas akan dipilih ketua, sekretaris, dan bendahara kelas. Jika banyaknya siswa di kelas tersebut adalah 15, berapa banyak susunan pengurus yang mungkin?
Banyaknya kemungkinan siswa terpilih menjadi ketua adalah 15.
Karena ketua sudah dipilih, tersisa 14 siswa.
Jika selanjutnya memilih sekretaris, banyaknya kemungkinan siswa terpilih menjadi sekretaris adalah 14 dan banyaknya kemungkinan siswa terpilih menjadi bendahara adalah 13.
Banyak susunan pengurus kelas yang mungkin adalah 15 x 14 x 13 = 2.730 cara. Atau dengan menggunakan rumus permutasi diperoleh:
P(15, 3) = 15!/(15 – 3)! = (15 x 14 x 13 x 12!)/12! = 15 x 14 x 13 = 2.730 cara.
7. Dalam suatu pertemuan, terdapat kursi yang disusun secara melingkar. Jika terdapat 7 kursi dan 7 orang dalam pertemuan tersebut, berapa banyak susunan tempat duduk yang mungkin?
Soal tersebut dapat diselesaikan dengan menggunakan konsep permutasi siklis. Dengan demikian, banyaknya susunan adalah (n – 1)! = (7 -1)! = 6! = 720 cara.
Rumus Kombinasi
Rumus kombinasi r objek dari n objek dapat dituliskan sebagai berikut.
C(n, r) = n!/(r! (n – r)!)
Keterangan:
- C(n, r) : permutasi r objek dari n objek yang ada
- n : banyaknya objek keseluruhan
- r : banyaknya objek yang diamati/diberi perlakuan
Untuk lebih jelasnya, bisa nonton video rumus pintar tentang kombinasi ya.
Selanjutnya, coba kerjakan soal mengenai kombinasi di bawah ini.
Contoh Soal Kombinasi
1. Dari 4 bus di terminal akan dipilih 2 bus untuk berangkat ke Yogyakarta. Berapakah cara memilih bus tersebut?
4C2 = 4! / (2! (4-2)!)
4C2 = (4×3×2×1) /((2×1)(2×1))
4C2 = (4×3) /(2×1))
4C2 = 12 / 2 = 6
Jadi, banyaknya cara untuk memilih bus yang berangkat ke Yogyakarta adalah 6 cara.
2. Rudi pergi ke kamar untuk mengambil 3 jenis buku. Jika di kamarnya terdapat 6 jenis buku, hitung banyaknya kombinasi tiga jenis buku yang mungkin dibawa oleh Rudi ?
6C3 = 6!/(3!(6-3)!)
6C3 = (6×5×4×3×2×1) / ((3×2×1)(3×2×1))
6C3 = (6×5×4) / (3×2×1)
6C3 = 5×4 = 20
Jadi, kombinasi tiga jenis buku yang mungkin dibawa oleh Rudi adalah 20 kombinasi.
3. Pada suatu arisan yang dihadiri 7 ibu. Ke tujuh ibu tersebut saling berjabat tangan satu sama lain. Hitunglah banyak jabat tangan yang terjadi?
7C2 = 7!/(2!(7-2)!)
7C2 = 7!/(2! 5!)
7C2 = (7×6×5×4×3×2×1) / ((2×1)(5×4×3×2×1))
7C2 = (7×6) / 2
7C2 = 21
Jadi, banyaknya jabat tangan yang terjadi adalah 21 jabat tangan.
4. Kepengurus RT terdiri dari 5 orang laki-laki dan 3 orang wanita akan dipilih 4 perwakilan untuk menghadiri upacara 17 Agustus. Hitung banyak cara memilih jika perwakilan terdiri dari 2 orang laki-laki dan 2 orang perempuan?
Cara memilih 2 laki-laki:
5C2 = 5!/(2!(5-2)!)
5C2 = 5!/(2! 3!)
5C2 = (5×4×3×2×1) / ((2×1)(3×2×1))
5C2 = (5×4) / 2
5C2 = 10
Cara memilih 2 perempuan
3C2 = 3!/(2!(3-2)!)
3C2 = 3!/ 2!
3C2 = (3×2×1) / (2×1)
3C2 = 3
Cara memilih 2 laki-laki dan 2 perempuan = 10 × 3 = 30
Jadi, banyaknya cara memilih perwakilan RT tersebut adalah 30 cara.
5. Tia ingin membeli 6 jenis boneka di toko yang menjual 9 jenis boneka. Jika 2 jenis boneka sudah pasti dibeli, berapa banyak kombinasi 6 boneka yang mungkin dibeli Tia?
Karena 2 jenis boneka sudah pasti dibeli, Tia tinggal memilih sisanya, yaitu 6-2 = 4 jenis boneka dari sisa jenis boneka yang belum dipilih, yaitu 9-2 =7, maka:
7C4 = 7!/(4!(7-4)!)
7C4 = 7!/ (4!3!)
7C4 = (7×6×5×4×3×2×1) / ((4×3×2×1)(3×2×1))
7C4 = (7×6×5) / (3×2×1)
7C4 = 7×5
7C4 = 35
Jadi, kombinasi 6 boneka yang mungkin dibeli Tia ada 35.
6. Linda akan mengambil 2 teko dan 3 mangkok dari lemari dapur yang menyimpan 6 teko dan 4 mangkok. Hitung banyak cara Linda bisa mengambil teko dan mangkok?
Banyak cara memilih teko:
6C2 = 6!/(2!(6-2)!)
6C2 = 6!/ (2!4!)
6C2 = (6×5×4×3×2×1) / ((2×1)(4×3×2×1))
6C2 = (6×5) / 2
6C2 = 15
Banyak cara memilih mangkuk:
4C3 = 4!/(3!(4-3)!)
4C3 = 4!/(3! 1!)
4C3 = (4×3×2×1) / ((3×2×1)(1))
4C3 = 4
Banyak cara memilih teko dan mangkuk = 15 × 4 = 60
Jadi, banyaknya cara Linda bisa mengambil teko dan mangkok adalah 60 cara.
7. Sebuah kelas akan memilih 4 putra dan 5 putri untuk menjadi paduan suara. Jumlah siswa di kelas tersebut adalah 20 orang. Jika terdapat 9 orang putra di kelas tersebut, berapakah banyak cara memilih paduan suara dari kelas tersebut!
Banyaknya siswa putra = 9
Banyaknya siswa putri = 20 – 9 = 11
Banyaknya cara memilih 4 dari 9 putra adalah 9C4
Banyaknya cara memilih 5 dari 11 putri adalah 11C5
Banyaknya cara memilih paduan suara = Banyaknya cara memilih putra × Banyaknya cara memilih putri
= 9C4 × 11C5
= 9!/(4!×(9-4)!) × 11!/(5!×(11-5)!)
= 9!/(4!×5!) × 11!/(5!×6!)
= 126 × 462
= 58212
Banyaknya cara memilih paduan suara dari kelas tersebut adalah 58212 cara.
8. Terdapat 8 orang dalam suatu kelompok. Jika 3 dari 8 orang tersebut akan dijadikan delegasi dalam suatu pertemuan internasional, berapa banyak susunan delegasi yang mungkin?
Permasalahan tersebut dapat diselesaikan dengan menerapkan rumus kombinasi karena dalam permasalahan tersebut urutan tidak diperhatikan.
C(8, 3) = 8!/(3! (8 – 3)!) = 8!/(3! x 5!) = (8 x 7 x 6 x 5!)/(3x 2 x 1 x 5!) = (8 x 7 x 6)/(3 x 2 x1) = 56 susunan delegasi.
9. Dalam suatu pesta terdapat 10 orang yang hadir dalam pesta tersebut. Jika setiap orang saling berjabat tangan antara satu dengan yang lain, berapa banyak jabat tangan yang dilakukan dalam pesta tersebut?
Penyelesaian soal ini bisa dilakukan dengan memasangkan dua orang yang saling berjabat tangan, sehingga dapat ditentukan dengan kombinasi 2 dari 10 orang.
C(10, 2) = 10!/(2! (10 – 2)!) = (10 x 9 x 8!)/(2! X 8!) = (10 x 9)/2 = 45 jabat tangan.
Dengan menggunakan cara yang lain juga diperoleh:
Misal terdapat 2 orang dalam pesta, maka banyak jabat tangan adalah 1.
Misal terdapat 3 orang dalam pesta, maka banyak jabat tangan adalah 1 + 2 = 3
Misal terdapat 4 orang dalam pesta, maka banyak jabat tangan adalah 1 + 2 + 3 = 6
Dan seterusnya, sehingga:
Jika terdapat 10 orang dalam pesta, maka banyak jabat tangan adalah
1 + 2 + 3 + . . . + 9 = 45 jabat tangan.
Mari kita simpulkan bersama.
Kesimpulan
- Permutasi dapat diartikan sebagai aturan pencacahan/penyusunan dengan memperhatikan urutan objek. Sedangkan kombinasi merupakan suatu aturan pencacahan/penyusunan tanpa memperhatikan urutan objek.
- Perbedaan permutasi dan kombinasi yaitu pada permutasi memperhatikan urutan objek, sedangkan pada kombinasi tidak.
- Rumus untuk permutasi adalah P(n, r) = n!/(n – r)!
- Rumus untuk permutasi siklis adalah (n – 1)!
- Rumus untuk kombinasi adalah C(n, r) = n!/(r! (n – r)!
Demikian artikel mengenai permutasi dan kombinasi kali ini. Semoga dapat memberikan tambahan wawasan dan pengetahuan bagi kalian semua. Baca juga Peluang.
