Halo semua! Pada kesempatan ini, kita akan belajar menyelesaikan soal persamaan kuadrat. Sebelum masuk ke contoh soal, mari kita refresh sejenak apa itu persamaan kuadrat.
Persamaan kuadrat secara sederhana dapat dipahami sebagai bentuk polinomial dengan pangkat tertinggi 2.
Bentuk umum persamaan kuadrat yaitu ax2 + bx + c = 0 dengan a ≠ 0.
Untuk lebih lengkapnya, silakan baca di Persamaan Kuadrat
Contoh Soal Persamaan Kuadrat & Jawabannya
1. Terdapat persamaan kuadrat: 1 – (6/x) + (9/x2) = 0. Maka, tentukan nilai 9/x
Dalam soal di atas, persamaan dalam bentuk pecahan sehingga Anda harus mengalikan x2 pada kedua ruas sehingga berbentuk x2 – 6x + 9 = 0. Dari persamaan ini, Anda bisa mencari akar-akar dari persamaan tersebut.
Bentuk sederhana dari persamaan kuadrat x2 – 6x + 9 adalah (x – 3)(x – 3). Sehingga di dapatkan nilai x=3. Anda dapat memasukkan nilai x ke dalam 9/x Hasil akhirnya adalah 3.
2. Sebuah persamaan kuadrat x2 + ax – 4 = 0 memiliki akar yaitu m dan n. Jika terdapat sebuah persamaan kuadrat m2 – 2mn + n2 = 8y. Maka tentukan nilai y
Untuk mengerjakan soal ini, Anda harus mempelajari sifat-sifat persamaan kuadrat terutama dalam hal akar-akar persamaan. Pertama, Anda harus mencari nilai m dan n terlebih dahulu.
Suatu persamaan kuadrat biasanya berbentuk Ax2 + Bx + C = 0. Dalam bentuk x2 + yx – 4 = 0, nilai A = 1, B = a, C = -4. Salah satu sifat akar persamaan kuadrat adalah pertambahan antara kedua akar sama dengan 
. Sehingga dapat Anda dapat tulis dalam bentuk seperti di bawah ini.
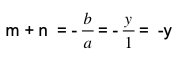
Kedua, jika kedua akar dikalikan maka hasilnya sama dengan 
, sehingga bentuknya dapat Anda tulis seperti berikut ini.
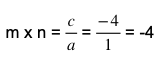
Setelah Anda mendapatkan nilai m+n dan m.n, selanjutnya Anda dapat menggunakan hasilnya pada persamaan m2 – 2mn + n2 = 8y . Persamaan ini bisa Anda sederhanakan seperti cara penyelesaian di bawah ini.
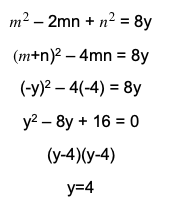
3. Diketahui persamaan kuadrat memiliki akar dengan X1 = (1- √3)dan X2 = (1+√3) Tentukan persamaan kuadratnya
Suatu persamaan kuadrat dibentuk oleh x2 –(x1+x2)x + x1x2. Jika diketahui X1 dan X2 maka Anda dapat melakukan penjumlahan dan perkalian akar untuk membentuk suatu persamaan kuadratnya.
x1+x2 = (1- √3) + (1+ √3) = 2
x1x2 = (1- √3) x (1+ √3) = -2
Sehingga persamaan kuadratnya adalah x2 -2x -2
4. Jika diketahui suatu persamaan memiliki bentuk akar p dan q dimana p dan q bernilai 2 kali akar persamaan x2 + 3x + 7 dikurangin 1. Bentuklah sebuah persamaan kuadrat baru menggunakan p dan q.
Untuk mengerjakan soal ini, Anda harus mencari akar-akar dari x2 + 3x + 7 terlebih dahulu. Sama seperti soal sebelumnya, Anda dapat menentukan akar melalui sifat penjumlahan dan perkalian akar-akar.
x1+x2 = = -3
x1x2 = = 7
Lalu identifikasi nilai p dan q dimana p = 2x1 – 1 dan q = 2x2 – 1. Sehingga Anda dapat melakukan penjumlahan dan perkalian akar p dan q.
p+q = (2x1 – 1) + (2x2 – 1) = 2(x1 + x2) – 2 = 2(-3) – 2 = -8
p.q = (2x1 – 1)( 2x2 – 1) = 4x1x2 – 2(x1+x2) +1 = 4(7) – 2(-3) + 1 = 35
Sehingga Anda dapat membuat persamaan baru menggunakan hasil operasi hitung di atas.
x2 + 8x + 35 = 0
5. Terdapat suatu persamaan
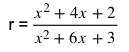
Tentukan nilai r jika akar persamaan tersebut adalah kembar
Untuk mengerjakan soal ini, Anda dapat mengali silang antara ruas kanan dan kiri. Kemudian Anda sederhanakan persamaan tersebut sehingga menjadi seperti di bawah ini.
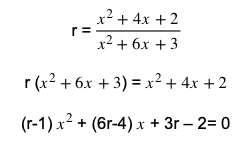
Suatu persamaan yang memiliki akar kembar artinya nilai D= 0.
D = 0
b2 – 4ac = 0
(6r-4)2 – 4(r-1)(3r-2) = 0
36r2 – 48r + 16 – 12r2 + 20r – 8 = 0
24r2 – 28r + 8 = 0
6r2 – 7r + 2 = 0
(3r – 2)(2r – 1) = 0
Sehingga di dapatkan nilai r = 2/3 dan 1/2
Sekian 5 Contoh soal tentang persamaan kuadrat. Semoga bermanfaat ya.