Pengertian Persamaan Linear
Persamaan aljabar disebut sebagai persamaan linear jika setiap suku dalam persamaan tersebut mengandung konstanta dan dikalikan dengan variabel tunggal.
Jika terdapat lebih dari satu persamaan linear, maka persamaan linear tersebut akan menjadi sebuah sistem.
Bentuk umum sistem persamaan linear adalah sebagai berikut:
a11x1 + a12x2 + a13x3+ … + a1nxn = C1
a21x1 + a22x2 + a23x3+ … + a2nxn = C2
:
an1x1 + an2x2 + an3x3+ … + annxn = Cn
atau dalam bentuk matriks dapat ditulis sebagai berikut:
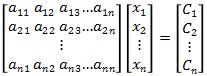
Setelah memahami apa itu persamaan linear, akan kita bahas beberapa macam sistem persamaan linear.
Sistem Persamaan Linear Satu Variabel
Sistem persamaan linear satu variabel adalah sistem persamaan dengan hanya terdapat sebuah variabel saja berpangkat 1. Bentuk umumnya sebagai berikut:
ax + b = 0
dengan a dan b adalah bilangan bulat bukan nol dan b konstanta. Baca juga Relasi dan Fungsi.
Contoh Soal Sistem Persamaan Linear Satu Variabel
Suatu hari Firdah hendak membuat rucuh mbawang untuk dua orang temannya. Untuk itu dia membeli 7 buah mbawang dan 1 kg gula merah. Jika harga 1 kg gula merah adalah Rp15.000,00 dan Firdah membayar Rp50.000,00, berapakah harga satu buah mbawang?
Jika harga 1 kg gula adalah Rp15.000,00 dan misalkan mbawang = x, maka sistem persamaan linearnya dapat dituliskan sebagai berikut:
7x + 15.000 = 50.000
Sehingga nilai x yang dimaksud adalah
7x + 15.000 = 50.000
x = 5.000
Sistem Persamaan Linear Dua Variabel
Berbeda dari sebelumnya, sistem persamaan linear dua variabel adalah sistem persamaan dengan variabel berjumlah dua berpangkat 1 satu. Bentuk umumnya sebagai berikut:
ax + by = c
dengan a dan b adalah bilangan bulat bukan nol dengan c adalah konstanta.
Contoh Soal Sistem Persamaan Linear Dua Variabel
Genta membeli 3 pensil dan 2 penghapus seharga Rp11.000,00, sedangkan Fitria membeli 1 pensil dan 6 penghapus dengan harga Rp17.000,00. Jika Annies membeli 5 pensil dan 15 penghapus, berapa uang minimal yang harus disiapkan Annies?
Misal pensil = x dan penghapus = y, maka sistem persamaan linearnya menjadi:
3x + 2y = 11.000
x + 6y = 17.000
kemudian persamaan pertama dikalikan dengan 3 menjadi:
9x + 6y = 33.000
x + 6y = 17.000 _
x = 2.000
Karena x = 2.000, maka y = 2.500
Sehingga jika Annies hendak membeli 5 pensil dan 15 penghapus, maka Annies setidaknya menyiapkan uang sebesar:
5x + 15y = 5(2.000) + 15(2.500)
= 10.000 + 37.500
= Rp47.500,00
Sistem Persamaan Linear Tiga Variabel
Sistem persamaan linear tiga variabel merupakan sistem persamaan dengan variabel berjumlah tiga berpangkat 1 satu. Bentuk umumnya sebagai berikut:
ax + by + cz = d
dengan a, b, dan c adalah bilangan bulat bukan nol dengan d adalah konstanta.
Contoh Soal Sistem Persamaan Linear Tiga Variabel
Sebuah perusahaan catering hendak mengirim pesanan pelanggan di kecamatan A, B, dan C. Perusahaan tersebut mengirimkan 6 paket 1 dan 10 paket 2 dengan harga Rp376.000,00 di Kecamatan A, 5 paket 2 dan 4 paket 3 dengan harga Rp241.000,00 di Kecamatan B, dan terakhir mengirimkan 2 paket 1, 3 paket 2, dan 2 paket 3 dengan harga Rp175.000,00. Berapakah harga dari tiap paket yang ditawarkan oleh perusahaan catering tersebut?
Misal paket 1 = a, paket 2 = b, dan paket 3 = c, maka sistem persamaan linearnya dapat dituliskan sebagai berikut:
6a + 10b = 376.000 … 1)
5b + 4c = 241.000 … 2)
2a + 3b + 2c = 175.000 … 3)
- Dari 1) dan 3)
6a + 10b = 376.000
2a + 3b + 2c = 175.000
Persamaan 3) dikalikan 3, maka menjadi:
6a + 10b = 376.000
6a + 9b + 6c = 525.000_ _
b – 6c = -149.000 … 4)
- Dari 2) dan 4)
5b + 4c = 241.000
5b – 30c = -745.000 _
c = 29.000
didapatkan c = 29.000, maka
5b + 4c = 241.000
5b = 241.000 – 116.000
b = 25.000
karena b = 25.000, maka
6a + 10b = 376.000
6a = 376.000 – 250.000
a = 21.000
Jadi, harga dari tiap paket yang ditawarkan oleh perusahaan catering tersebut adalah:
Paket 1 = Rp21.000,00; Paket 2 = Rp25.000,00; Paket 3 = Rp29.000,00
Untuk latihan soal lebih lengkap, Baca juga Contoh Soal SPLTV
