Pada pertemuan kali ini kita akan membahas kumpulan latihan soal untuk materi Transformasi Geometri. Di bawah ini terdapat beberapa contoh soal Transformasi Geometri beserta jawaban dan pembahasannya yang sudah kami kumpulkan untuk anda pelajari. Mari kita simak pembahasannya.
Sekilas tentang Transformasi Geometri
Transformasi geometri adalah perubahan posisi dari posisi awal ke posisi yang lainnya. Perubahan posisi tersebut menggunakan aturan tertentu yang mengakibatkan posisi suatu objek berubah.
Transformasi geometri terbagi atas pergeseran (translasi), pencerminan (refleksi), perputaran (rotasi), dan perkalian (dilatasi).
Untuk lebih lengkapnya, silakan baca di Transformasi Geometri.
Contoh Soal Transformasi Geometri dan Jawabannya
Di bawah ini terdapat beberapa contoh soal transformasi geometri beserta pembahasannya yang sudah kami kumpulkan. Silakan dipelajari dan dipahami untuk meningkatkan pemahaman anda tentang transformasi geometri.
1. Tentukan koordinat titik A jika A’ (13, -20) merupakan bayangan titik A karena translasi B (10, -7), yaitu:
Misal A = (x, y), maka
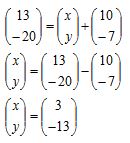
Jadi, koordinat titik A adalah (3, -13).
2. Diketahui B’(8, 4) merupakan bayangan titik B(x, y) yang dirotasikan pada pusat (0, 0) sebersar 90o. Berapakah nilai 2x + y?
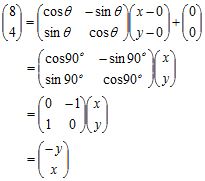
Diperoleh x = 4 dan y = -8. Maka:
2x + y = 2 (4) + (-8)
2x + y = 8 – 8
2x + y = 0
Jadi, nilai 2x + y adalah 0.
3. Diketahui C(-4, 7) direfleksikan terhadap garis y = -x. Maka koordinat bayangan titik C adalah …
Misal C’(x, y) adalah koordinat bayangan titik C, maka:
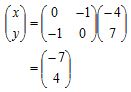
Jadi, koordinat bayangan titik C adalah (-7, 4).
4. Tentukan bayangan titik D(3, 2) jika dilatasikan terhadap pusat (-1, -2) dengan skala -3!
Misal
D’(x, y) adalah bayangan titik D
Maka
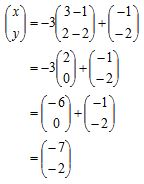
Jadi, bayangan titik D adalah (-7, -2).
5. Tentukan bayangan titik E(3, 7) jika direfleksikan terhadap sumbu x lalu dilanjutkan dengan dilatasi pada pusat (0, 0) dengan skala 2.
Misal:
E’(p, q) merupakan bayangan titik E jika direfleksikan terhadap sumbu x, maka
E’’(r, s) merupakan bayangan titik E’ jika dilatasikan pada pusat (0, 0) dengan skala 2.
Refleksi titik E pada sumbu x adalah
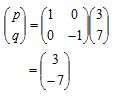
Dilatasi titik E’ pada pusat (0, 0) dengan skala 2 adalah
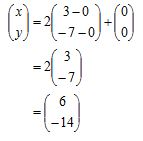
Jadi, bayangan titik E(3, 7) jika direfleksikan terhadap sumbu x lalu dilanjutkan dengan dilatasi pada pusat (0, 0) dengan skala 2 adalah (6, -14)
Demikian beberapa latihan soal transformasi geometri dengan jawaban dan pembahasannya dapat kami rangkum kali ini. Silakan dipelajari dan dipahami agar anda bisa meningkatkan pemahaman anda seputar materi transformasi geometri.
Sekian dari rumuspintar, selamat belajar.
