Pada artikel kali ini akan membahas mengenai kalkulus. Kalkulus merupakan salah satu materi lanjutan dalam matematika.
Dalam materi kalkulus ini,akan dipelajari mengenai sutau fungsi beserta turunannya. Dalam materi kalkulus ini juga dipelajari mengenai karakteristik suatu persamaan.
Berikut akan dijelaskan mengenai pengertian dari kalkulus.
Pengertian Kalkulus
Kalkulus merupakan salah satu topik bahasan dalam matematika. Topik pembahasan kalkulus meliputi konsep limit, diferensial atau turunan, serta integral atau anti-turunan.
Pembahasan mengenai konsep-konsep materi dalam kalkulus akan dijelaskan pada bagian yang lain.
Berikutnya akan disebutkan beberapa contoh penerapan kalkulus dalam kehidupan sehari-hari.
Kalkulus dalam Kehidupan Sehari-hari
Kalkulus memiliki beragam penerapan dalam kehidupan sehari-hari. Matematika sebagai salah satu induk ilmu pengetahuan sangat dibutuhkan dalam bidang lain.
Beberapa penerapan kalkulus dalam bidang lain antara lain:
- Pada bidang fisika, khusunya terkait mekanika, kalkulus sangat diperlukan untuk menyelesaikan perhitungan-perhitungan dengan menerapkan konsep kalkulus.
- Dalam bidang statistika dan teori peluang juga terdapat perhitungan dengan menerapkan konsep kalkulus (integral).
- Dalam bidang ekonomi, kalkulus dapat digunakan untuk menentukan biaya marginal (kalkulus diferensial).
Dan masih banyak lagi bidang-bidang yang menerapkan konsep kalkulus.
Selanjutnya akan dijelaskan mengenai kalkulus dasar.
Kalkulus Dasar
Penjelasan mengenai kalkulus dasar pada bagian ini yaitu konsep mengenai limit, turunan (diferensial), dan anti-turunan (integral).
Limit
Misalkan terdapat suatu fungsi f(x). Limit dapat didefinisikan sebagai suatu nilai fungsi untuk nilai x mendekati suatu bilangan tertentu. Limit dapat dirumuskan sebagai berikut.
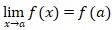
Keterangan:
- x : variabel
- a : suatu bilangan
- f(x) : fungsi dengan variabel x
- f(a) : nilai limit fungsi x mendekati a.
Baca Selengkapnya di Limit Fungsi
Selanjutnya akan dibahas mengenai turunan (diferensial).
Turunan (Diferensial)
Turunan merupakan lanjutan dari konsep limit. Misalkan terdapat suatu fungsi f(x).
Turunan dapat didefinisikan sebagai suatu perhitungan terhadap perubahan nilai f(x) seiring dengan perubahan dari nilai x.
Turunan dari suatu fungsi f(x) disimbolkan dengan f’(x). Misalkan terdapat f(x) = axn, maka turunan dari fungsi tersebut adalah
f’(x) = anxn-1
Keterangan:
- f(x) : fungsi dengan variable x
- f’(x) : turunan fungsi f(x)
Baca Selengkapnya di Turunan
Selanjutnya akan dibahas mengenai anti-turunan atau integral.
Anti-turunan (Integral)
Pernahkah kalian mendengar mengenai integral? Integral merupakan kebalikan dari turunan.
Misalkan terdapat suatu fungsi f(x). Integral dari fungsi f(x), disimbolkan dengan F(x) yaitu sebagai berikut.
F(x) = ∫ f(x)
Keterangan:
- F(x) : integral dari f(x)
- f(x) : fungsi dengan variable x.
Misalkan terdapat fungsi f(x) = axn. Integral dari fungsi tersebut adalah
F(x) = ∫ axn = a/(n + 1) xn+1 + C
Keterangan:
- F(x) : integral dari suatu fungsi
- axn : fungsi dengan koefisien a, variabel x, dan pangkat n.
- C : konstanta
Baca Selengkapnya di Integral
Untuk lebih memahami mengenai kalkulus, perhatikan beberapa contoh soal kalkulus berikut.
Contoh Soal Kalkulus
1. Tentukan nilai dari limit berikut.
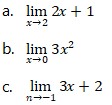
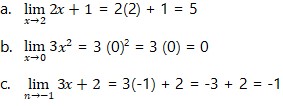
2. Tentukan turunan dari fungsi berikut.
- a. f(x) = 2x
- b. g(x) = -4x3
- c. h(x) = x3 + 4x2 + 2x
a. f’(x) = 2 (1) x1 – 1 = 2x0 = 2
b. g’(x) = -4 (3) x3 – 1 = -12x2
c. h’(x) = 3x3 – 1 + 4 (2) x2 – 1 + 2 (1) x1 – 1
h’(x) = 3x2 + 8x + 2
3. Tentukan integral dari fungsi f(x) = 6x2 + 2x.
F(x) = ∫6x2 + 2x = 6/(2 + 1) x2 + 1 + 2/(1 + 1) x1 + 1 + C
F(x) = 6/3 x3 + 2/2 x2 + C
F(x) = 2x3 + x2 + C
Mari kita simpulkan bersama.
Kesimpulan
Kalkulus merupakan salah satu topik bahasan dalam matematika. Topik pembahasan kalkulus meliputi konsep limit, diferensial atau turunan, serta integral atau anti-turunan.
Kalkulus dasar meliputi konsep limit, turunan (diferensial), dan anti-turunan (integral).
Misalkan terdapat suatu fungsi f(x), limit dari fungsi tersebut untuk nilai x mendekati a yaitu:
![]() .
.
Misalkan terdapat f(x) = axn, maka turunan dari fungsi tersebut adalah f’(x) = anxn-1.
Misalkan terdapat fungsi f(x) = axn. Integral dari fungsi tersebut adalah F(x) = ∫axn = a/(n + 1) xn+1 + C.
Bagaimana penjelasan mengenai kalkulus di atas? Apakah kalian dapat memahami materi tersebut dengan mudah?
Semoga penjelasan di atas dapat menambah wawasan kalian mengenai kalkulus. Terima kasih.
