Persamaan Garis Lurus & Singgung: Pengertian, Rumus, dan Contoh Soal

Materi yang akan kita bahas adalah mengenai persamaan garis.

Terdapat berbagai macam bentuk garis. Terdapat garis lurus, garis lengkung, kurva, dan lain-lain. Garis-garis tersebut dapat dilukis pada koordinat kartesius.

Masing-masing garis yang telah dilukis pada koordinat kartesius memiliki persamaan garis.

Oleh karena itu, pada bagian di bawah ini akan dibahas mengenai persamaan garis.

Definisi Persamaan Garis

Seperti yang telah disebutkan pada bagian sebelumnya, garis memiliki berbagai macam bentuk.

Garis-garis dengan bentuk berbeda yang dilukis pada koordinat kartesius memiliki persamaan garis yang berbeda pula.

Lalu apa itu persamaan garis?

Secara sederhana, persamaan garis merupakan representasi simbolik suatu garis yang dilukis pada koordinat kartesius. Persamaa garis ditandai dengan tanda “ = “.

Contoh persamaan garis antara lain 2x + 3y – 4 = 0, x² + 2x + 3 = 0,  x² + y² = 25.

Masing-masing persamaan garis tersebut mewakili persamaan garis lurus, persamaan kurva/parabola, dan persamaan lingkaran.

Bagian berikutnya akan dibahas mengenai penerapan persamaan garis.

Persamaan Garis dalam Kehidupan Sehari-hari

Apakah kalian dapat menemukan contoh-contoh penerapan persamaan garis dalam kehidupan sehari-hari?

Beberapa contoh penerapan persamaan garis misalnya seperti penghitungan sistem persamaan linear dua variable dengan menggunakan grafik (menggunakan konsep persamaan garis lurus), percobaan pelemparan bola yang membentuk kurva (persamaan kuadrat), dan mobil yang melewati lintasan berbentuk lingkaran (persamaan lingkaran).

Pada bagian selanjutnya akan dijelaskan mengenai rumus persamaan garis.

Rumus Persamaan Garis

Beberapa rumus persamaan garis dalam pembahasan berikut antara lain persamaan garis lurus dan persamaan garis singgung.

Persamaan garis singgung yang akan dibahas mengenai persamaan garis singgung kurva dan persamaan garis singgung lingkaran.

Persamaan Garis Lurus

Bentuk umum persamaan garis lurus yaitu ax + by + c = 0. Persamaan garis lurus dapat dilukis dalam koordinat kartesius.

Bagaimana cara menentukan persamaan garis dari suatu grafik pada koordinat kartesius?

Coba perhatikan gambar berikut.

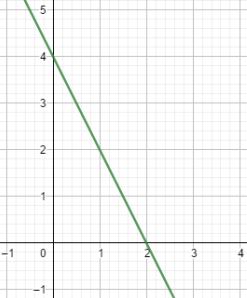
Pada grafik di atas terdapat garis lurus yang melalui koordinat (0, 4) dan (2, 0). Persamaan garis melalui dua titik dirumuskan dengan

Misalkan (x₁, y₁) = (0, 4) dan (x₂, y₂) = (2, 0)

(y – y₁)/(y₂ – y₁) = (x – x₁)/(x₂ – x₁)

(y – 4)/(0 – 4) = (x – 0)/(2 – 0)

(y – 4)/(-4) = x/2

2(y – 4) = – 4x

2y – 8 = -4x

4x + 2y – 8 = 0

Persamaan garis tersebut dapat disederhanakan menjadi 2x + y – 4 = 0.

Keterangan:

• x, y : variabel
• (x₁, y₁); (x₂, y₂) : titik-titik yang dilalui oleh garis

Selanjutnya akan dibahas mengenai persamaan garis singgung.

Persamaan Garis Singgung

Persamaan garis singgung pada pembahasan kali ini akan dibagi menjadi dua yaitu persamaan garis singgung kurva dan persamaan garis singgung lingkaran.

Walaupun lingkaran merupakan salah satu kurva tertutup, namun kali ini yang akan dipelajari adalah garis singgung kurva (persamaan kuadrat) dan lingkaran.

Persamaan Garis Singgung Kurva

Perhatikan gambar berikut.

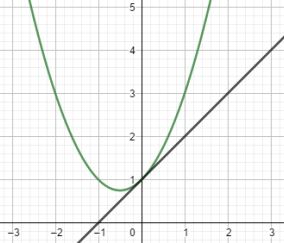
Pada gambar di atas terdapat kurva dan garis singgungnya.

Secara umum, kurva kuadrat memiliki persamaan garis yaitu ax² + bx + c = 0.

Persamaan garis singgung kurva yang menyinggung kurva di titik (x₁, y₁) dengan gradien m yaitu

y – y₁ = m (x – x₁)

Contohnya pada gambar di atas. Pada kurva tersebut, persamaan garisnya adalah x² + x + 1 = 0. Persamaan garis singgung yang melalui (0, 1) dan gradient 1 yaitu

Pertama kita cek apakah titik (0, 1) berada pada kurva atau tidak.

(0, 1) à (0)² + 0 + 1 = 1 (benar) sehingga titik (0, 1) terdapat pada kurva. Sehingga:

y – y₁ = m (x – x₁)

y – 0 = 1 (x – 1)

y = x – 1

x – y – 1 = 0.

Jadi persamaan garis singgungnya adalah x – y – 1  = 0.

Keterangan:

• x, y : variabel
• (x₁, y₁): titik yang dilalui oleh garis singgung
• m  : gradien garis singgung

Selanjutnya akan dibahas mengenai persamaan gari singgung lingkaran.

Persamaan Garis Singgung Lingkaran

Secara umum persamaan lingkaran adalah x² + y² + Ax + By + C = 0. Jika pusat lingkaran adalah (0, 0), maka persamaan lingkarannya yaitu x² + y² = r².

Perhatikan gambar berikut.

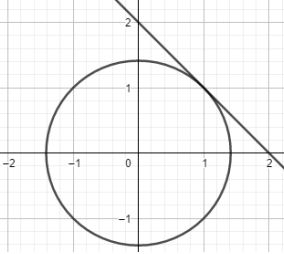
Pada gambar di atas terdapat garis singgung yang menyinggung lingkaran di satu titik.

Terdapat lingkaran dengan persamaan x² + y² = 2 dan titik singgung pada koordinat (1, 1). Bisa kita ketahui bahwa gradient garis tersebut adalah -1.

Persamaan garis singgungnya adalah

y = mx ± r √(1 + m²)

y = -1(x) ± (√2) √(1 + (-1)²)

y = -x ± 2

sehingga persamaan garis singgungnya

y = -x + 2  atau y = -x – 2

x + y – 2 = 0  atau  x + y + 2 = 0

Ternyata x + y + 2 = tidak memenuhi karena jika kita substitusikan (1, 1) ke dalam persamaan garis singgung 1 + 1 + 2 ≠ 0, sehingga persamaan garis singgung lingkaran yang memenuhi adalah x + y – 2 = 0.

Keterangan :

• x, y : variabel
• m : gradient garis singgung
• r  : jari-jari lingkaran

Kerjakan soal berikut untuk mengetahui pemahamanmu. Baca juga Persamaan Linear.

Contoh Soal Persamaan Garis

1. Persamaan garis yang melalui titik (3, 1) dan (2, 0) adalah . . .  .

2. Persamaan garis singgung lingkaran x² + y² = 5 pada titik (4, 1)  dan gradien -2 adalah … .

Mari kita simpulkan bersama.

Kesimpulan

• Persamaan garis merupakan representasi simbolik suatu garis yang dilukis pada koordinat kartesius.
• Rumus persamaan garis lurus melalui dua titik adalah y – y₁ = m (x – x₁)
• Rumus persamaan garis singgung kurva melalui titik (x₁, y₁) dan gradien m adalah

y – y₁ = m (x – x₁)

• Rumus persamaan garis singgung lingkaran x² + y² = r²  dengan gradien m adalah

y = mx ± r √(1 + m²)

Demikian penjelasan mengenai persamaan garis. Semoga bermanfaat. Baca juga Vektor.