Pengertian
Relasi berarti hubungan antara (domain) daerah asal dan (kodomain) daerah kawan, sedangkan fungsi adalah hubungan yang memasangkan anggota daerah asal dengan tepat satu anggota daerah lawan dengan aturan khusus.
Berikut adalah bentuk diagram suatu fungsi tertentu:
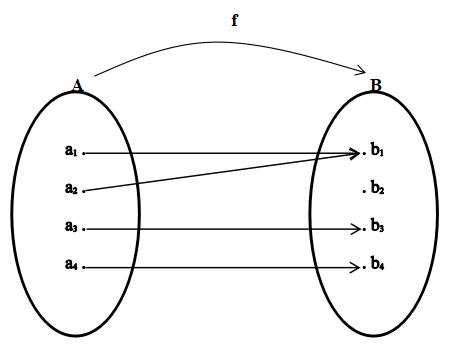
Dari gambar di atas dapat kita tahu bahwa diagram tersebut merupakan diagram relasi dan fungsi dari dua buah himpunan yaitu A = {a1, a2, a3, a4} dan B = {b1, b2, b3, b4}.
Grafik fungsi
Selain dibuat diagram seperti yang dijelaskan sebelumnya, sebuah fungsi dapat diperlihatkan menggunakan grafik tertentu.
Grafik fungsi sendiri adalah sebuah representasi visual atau penggambaran dari sebuah fungsi pada diagram x-y.
Grafik fungsi dapat berfungsi sebagai alat yang membantu untuk memudahkan seseorang dalam memahami suatu fungsi.
Untuk menggambar sebuah grafik fungsi, cara termudah adalah memasukkan nilai x (daerah asal) pada f(x) atau y (daerah kawannya).
Grafik Fungsi Kuadrat
Grafik fungsi kuadrat pada dimensi dua memiliki bentuk berupa kurva cekung maupun cembung.
Ciri khas lainnya dari fungsi kuadrat adalah memiliki pangkat tertinggi 2 pada variabel dalam fungsi tersebut dengan bentuk fungsi:
y = ax2 + bx + c
dengan y = f(x) = variabel terikat, x = variabel bebas, a dan b koefisien dan c konstanta. Cara mudah menggambar grafik fungsi kuadrat adalah sebagai berikut:
1. Menentukan parabola yang terbentuk terbuka ke atas (cekung) atau terbuka ke bawah (cembung). Jika a>0 maka cekung, jika a<0 maka sebaliknya
2. Menentukan titik potong dengan sumbu x, dengan cara memisalkan y = f(x) = 0
3. Menentukan titik puncaknya yaitu dengan mencari absisnya menggunakan rumus 
. Kemudian mencari ordinatnya menggunakan f(xpuncak) , sehingga didapatkan koordinat puncak yaitu:
4. Mencari beberapa koordinat yang dapat dipakai untuk membantu menggambar grafik. Baca juga Persamaan Kuadrat.
Contoh Soal Relasi dan Fungsi
Buatlah grafik fungsi kuadrat y = x2 – 4x + 4!
a = 1, b = –4, c = 4
karena a = 1 > 0, maka grafik terbuka ke atas atau cekung.
Misalkan y = 0, maka
x2 – 4x + 4 = 0
(x – 2)(x – 2) = 0
x = 2
selanjutnya akan dicari koordinat titik puncak:
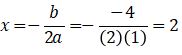
f(2) = 22 – 4.2 + 4 = 0
sehingga koordinat puncaknya (x, y) = (2, 0)
dari informasi yang didapatkan, maka grafik fungsinya adalah sebagai berikut:
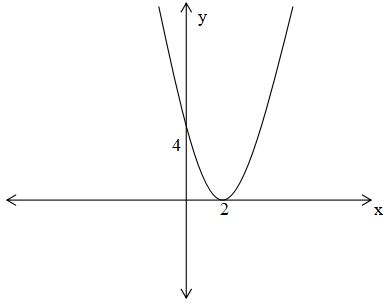
Fungsi invers
Fungsi invers adalah sebuah fungsi yang merupakan kebalikan dari fungsi tersebut. Dari arti katanya, fungsi invers berarti fungsi kebalikan.
Misalkan terdapat f suatu fungsi dari A ke B, jika g merupakan suatu fungsi dari B ke A dan memenhi sifat:
f(f(b)) = b ˄ g(f(a)) = a; Ɐ(a∈A ˄ b∈B)
maka g disebut fungsi invers dari f dan dapat ditulis dengan g = f-1.
Contoh Soal Fungsi Invers
Tentukan invers dari f(x) = 3x – 4!
f(x) = 3x – 4
3x = f(x) + 4
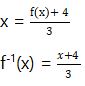
Demikian pembahasan tentang relasi dan fungsi. Semoga bermanfaat. Baca juga Diagram.