√ Mean, Median, Modus (Pengertian, Rumus, Soal)

Pada artikel kali ini akan dibahas mengenai mean, median, dan modus. Kita sering menjumpai berbagai jenis data dalam kehidupan sehari-hari.

Berbagai jenis data tersebut diolah dan dipublikasikan agar memberikan informasi yang berguna. Beberapa macam pengolahan data seperti mean, median, dan modus.

Berikut penjelasan mengenai mean, median, dan modus.

Contents show

Pengertian Mean, Median, dan Modus

Dalam statistika dikenal adanya ukuran pemusatan data. Beberapa ukuran pemusatan data yang perlu diketahui adalah mean, median, dan modus.

Apa saja mean, median, dan modus itu?

Mean dapat diartikan sebagai nilai rata-rata suatu kelompok data. Median adalah nilai tengah data setelah diurutkan. Sedangkan modus merupakan nilai yang sering muncul dalam suatu kelompok data.

Selanjutnya akan disampaikan mengenai penerapan mean, median, dan modus.

Penerapan Mean, Median, dan Modus

Mean, median, dan modus sangat diperlukan dalam menganalisis suatu hasil atau pengumpulan data.

Setelah data diperoleh/dikumpulkan, langkah selanjutnya adalah data diolah dengan metode statistik.

Misalkan pada kasus nilai ulangan matematika. Penerapan mean (rata-rata) dapat ditunjukkan saat menentukan berapa banyak siswa yang mendapatkan nilai di atas rata-rata nilai kelas.

Median digunakan apabila guru ingin membagi kelas menjadi dua kelompok berdasarkan urutan nilai.

Modus dapat digunakan oleh guru untuk mengetahui berapa banyak siswa yang memperoleh nilai tertentu atau menentukan frekuensi terbanyak dari suatu data.

Selanjutnya akan dijelaskan mengenai rumus terkait mean, median, dan modus.

Rumus Mean, Median dan Modus

Pada bagian di bawah ini akan dijelaskan beberapa rumus yaitu yang berkaitan dengan mean, median, dan modus.

Rumus Mean

Pada bagian sebelumnya telah dijelaskan bahwa mean merupakan nilai rata-rata suatu data. Nilai rata-rata merupakan hasil bagi antara jumlah nilai keseluruhan dengan banyaknya data yang diolah. Secara matematis, mean (nilai rata-rata) dapat dituliskan sebagai

Rumus di atas merupakan rumus menentukan mean (nilai rata-rata) pada data tunggal. Selanjutnya akan dijelaskan rumus mean data kelompok.

Rumus Mean Data Kelompok

Sedikit berbeda dengan rumus mean (nilai rata-rata) pada data tunggal, rumus mean untuk data kelompok dirumuskan sebagai berikut.

Rumus Median

Cara menentukan median pada data tunggal cukup mudah.

Kita dapat mengurutkannya dari data terkecil ke data terbesar. Jika banyak data ganjil tentu kita langsung bisa menentukan nilai tengahnya.

Bagaimana jika banyaknya data genap?

Pada data tunggal untuk menentukan median yaitu:

Misalkan banyaknya data n, jika n ganjil maka median ditentukan dengan

Med = x_n/2

Jika banyaknya data genap, maka

Akan dijelaskan mengenai median data kelompok.

Rumus Median Data Kelompok

Median data kelompok dapat ditentukan jika kita telah mengetahui kelas mediannya. Carilah kelas data yang memuat data nilai tengah. Median data kelompok dapat ditentukan dengan

Med = t_b + ((n/2) – F_kum)/f_i) k

Keterangan:

Med : median
t_b : tepi bawah kelas median
n : banyaknya data
F_kum : frekuensi kumulatif sebelum kelas median
f_i : frekuensi kelas median
K : panjang kelas

Selanjutnya akan dibahas mengenai modus atau data yang sering muncul.

Rumus Modus

Untuk menentukan modus, biasanya pada data tunggal dibuat tabel frekuensi data tunggal agar memudahkan dalam menentukan frekuensi tiap data, lalu temukan data dengan frekuensi terbesar.

Rumus Modus Data Kelompok

Pada data berkelompok, modus dapat ditentukan dengan

Mo = t_b + (d₁/ (d₁ + d₂)) k

Keterangan:

Mo : modus data kelompok
t_b : tepi bawah kelas modus
d₁ : frekuensi kelas modus dikurangi frekuensi kelas sebelumnya
d₂ : frekuenso kelas modus dikurangn frekuensi kelas sesudahnya
k : panjang kelas

Untuk mengetahui seberapa jauh kemampuanmu mengenai mean, median, dan modus, kerjakan soal berikut. Baca juga Persamaan Kuadrat.

Contoh Soal Mean, Median, dan Modus

Perhatikan data berikut untuk mengerjakan soal nomor 1 – 3.

Nilai	Frekuensi
10 – 20	2
21 – 31	8
32 – 42	15
43 – 53	7
54 – 64	10
65 – 75	3

Berdasarkan data tersebut, tentukan

Mean dari data tersebut.
Median dari data tersebut.
Modus data tersebut

Pembahasan

Keterangan tambahan yang diperlukan dengan menghitung informasi yang diperlukan

Nilai	Frekuensi	F_{_kum}	x_{_i}	f_{_i} x x_{_i}
10 – 20	2	2	15	30
21 – 31	8	10	26	208
32 – 42 *	15	25	37	555
43 – 53	7	32	48	336
54 – 64	10	42	59	590
65 – 75	3	45	70	210

*) merupakan kelas median dan kelas modus

Mean

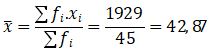
Median

Med = t_b + (((n/2) – F_kum)/f_i) k

Med = 31,5 + (((45/2) – 10)/15) 11

Med = 31,5 + 9, 17

Med = 40,67

Modus

Mo = t_b + (d₁/ (d₁ + d₂)) k

Mo = 31,5 + (7/(7 + 8)) 11

Mo = 31,5 + 5,13

Mo = 36,63

Mari kita simpulkan materi di atas.

Kesimpulan

Mean merupakan nilai rata-rata suatu data. Mean data kelompok dapat dihitung dengan

Median merupakan nila tengah dari data yang diurutkan. Median dapat ditentukan dengan Med = t_b + (((n/2) – F_kum)/f_i) k
Modus merupakan suatu nilai yang sering muncul. Modus suatu data dapat ditentukan dengan Mo = t_b + (d₁/ (d₁ + d₂)) k

Demikian artikel kali ini ditulis. Semoga tulisan ini dapat bermanfaat. Baca juga Himpunan.