Himpunan: Pengertian, Macam, Operasi, Contoh Soal

Pada pembahasan kali ini, kita akan belajar bersama-sama  mengenai himpunan.

Pernahkah kalian mengikuti suatu perkumpulan atau kelompok ekstrakurikuler di sekolah? Atau pernahkah kalian mengelompokkan suatu objek/benda tertentu.

Pengelompokan kegiatan ekstrakurikuler biasanya dilakukan sesuai dengan minat. Misalkan siswa yang gemar bermain sepakbola akan mengikuti ekstrakurikuler sepakbola, sehingga dalam satu kelompok ekstrakurikuler pasti merupakan kumpulan siswa-siswa yang gemar bermain sepakbola.

Begitu juga dengan perkumpulan/kelompok yang lainnya. Ketika kita mengelompokkan suatu benda/objek, kita akan mengelompokkannya berdasarkan sifat/ciri-ciri/kriteria tertentu sehingga dalam satu kelompok berisi objek/benda yang memiliki kesamaan ciri dan sifat.

Kegiatan pengelompokan tersebut akan berkaitan dengan himpunan. Untuk memahami mengenai konsep himpunan, perhatikan penjelasan berikut.

Pengertian Himpunan

Himpunan merupakan sekumpulan objek-objek yang didefinisikan secara jelas. Maksud dari didefinisikan secara jelas yaitu objek-objek tersebut dapat diukur (tidak relatif).

Anggota dari himpunan dituliskan di dalam kurung kurawal “{ … }. Beberapa contoh himpunan yaitu sebagai berikut.

• Himpunan siswa kelas VII SMP Juara.
• Himpunan siswa gemar bermain piano.
• Himpunan siswa dengan tinggi badan lebih dari 160 cm.
• Himpunan binatang berkaki empat.
• Himpunan bilangan prima kurang dari 10.

Semua contoh himpunan di atas merupakan himpunan, karena himpunan di atas terukur dan dapat didefinisikan dengan jelas.

Dapatkah kalian menyebutkan contoh himpunan yang lainnya?

Berikut disajikan contoh yang bukan merupakan himpunan.

• Himpunan siswa yang pandai.
• Himpunan mobil mewah.
• Himpunan warna yang indah.

Contoh-contoh di atas bukan merupakan himpunan karena pengelompokan tidak didefinisikan secara jelas. Pandai, mewah, dan indah merupakan kata sifat yang relatif (tidak dapat diukur secara jelas).

Selanjutnya akan dijelaskan mengenai contoh penerapan himpunan.

Himpunan dalam Kehidupan Sehari-hari

Himpunan banyak digunakan untuk mengelompokkan beberapa objek dengan ciri tertentu atau sejenis.

Misalnya dalam menyebutkan beberapa hewan berkaki empat, biasanya kita menyebutkannya dengan mendaftar atau membuat list.

Nah, selain dengan cara tersebut, kita dapat meyebutkannya dengan menggunakan himpunan. Selanjutnya akan dibahas mengenai himpunan kosong.

Himpunan Kosong

Apa yang dimaksud dengan himpunan kosong? Himpunan kosong merupakan himpunan yang tidak memiliki anggota. Himpunan kosong disimbolkan dengan tanda “{ }” atau “∅”. Beberapa contoh himpunan kosong yaitu sebagai berikut.

• Himpunan bilangan prima genap lebih dari 2.
• Himpunan nama hari yang berawalan huruf P.

Contoh himpunan di atas merupakan himpunan kosong, karena himpunan di atas tidak memiliki elemen atau anggota.

Selanjutnya akan dijelaskan mengenai himpunan semesta.

Himpunan Semesta

Apakah kalian mengetahui mengenai himpunan semesta? Himpunan semesta merupakan himpunan semua objek yang menjadi pembicaraan. Himpunan semesta dilambangkan dengan ”S”.

Himpunan Bagian

Dalam himpunan semesta, terdapat beberapa bagian atau kelompok himpunan yang merupakan bagian dari himpunan semesta.

Himpunan tersebut kita beri nama dengan himpunan bagian. Himpunan bagian memuat elemen-elemen/anggota yang terdapat dalam himpunan semesta.

Misalkan terdapat himpunan semesta sebagai berikut.

S = {a, b, c, d}

Himpunan bagian dari himpunan semesta di atas adalah.

Himpunan bagian: { }, {a}, {b}, {c}, {d}, {a, b}, {a, c}, {a, d}, {b , c}, {b, d}, {c, d}, {a, b, c}, {a, b, d}, {a, c, d}, {b, c, d}, {a, b, c, d}.

Himpunan bagian di atas terdiri dari himpunan kosong, himpnan bagian yang memuat satu anggota, himpunan bagian yang memuat dua anggota, himpunan bagian yang memuat tiga anggota, dan himpunan bagian yang memuat empat anggota.

Selanjutnya akan dijelaskan mengenai operasi himpunan. Baca juga Peluang.

Operasi Himpunan

Operasi himpunan yang akan dibahas dalah bagian ini adala operasi irisan dan gabungan. Irisan dalam himpunan disimbolkan dengan “Ո” dan gabungan dalam himpunan disimbolkan dengan “”. Perhatikan contoh berikut.

Misalkan terdapat dua himpunan

A = {2, 3, 5, 7, 11}

B = {1, 3, 5, 7, 9, 11}

Irisan dan gabungan dua himpunan tersebut yaitu:

A Ո B = {3, 5, 7, 11}

A Ս B = {1, 2, 3, 5, 7, 9, 11}

Selanjutnya akan dijelaskan mengenai himpunan penyelesaian.

Himpunan Penyelesaian

Himpunan penyelesaian secara sederhana dapat diartikan sebagai himpunan yang memuat solusi dari suatu permasalahan atau pembahasan.

Pada materi sebelumnya kalian sudah belajar mengenai bentu-bentuk operasi aljabar sederhana dan penyelesaiannya.

Dalam menuliskan solusi operasi aljabar sederhana, kalian dapat menggunakan himpunan penyelesaian ini. Perhatikan contohnya.

Misalkan terdapat operasi aljabar sebagai berikut.

6x – 2 < 3x + 7, x adalah bilangan asli.

Penyelesaian soal di atas adalah

6x – 3x < 7 + 2

3x < 9

x < 3

Sehingga, himpunan penyelesaiannya yaitu {1, 2}

Kerjakan soal berikut untuk meningkatkan pengetahuanmu mengenai himpunan. Baca juga Permutasi dan Kombinasi.

Contoh Soal Himpunan

1. Tentukan pernyataan di bawah ini termasuk ke dalam himpunan atau bukan himpunan.

• Himpunan siswa gemar bulutangkis.
• Himpunan siswa perempuan suka warna yang indah.
• Himpunan siswa yang pandai di kelas VII.
• Himpunan mobil berwarna bagus.
• Himpunan warna pelangi.

2. Berikan contoh himpunan kosong.

3. Terdapat himpunan semesta S = {M, A, T}. Tuliskan himpunan bagiannya.

4. Tuliskan himpunan penyelesaian dari operasi aljabar berikut.

2x – 1 < x + 3, x merupakan bilangan cacah.

5. Diketahui sebuah himpunan M = {1,2,3,4,5,6,7}. Berapa banyak himpunan bagian M yang banyak anggotanya ada 4?

Pembahasan

Untuk membentuk himpunan bagian yang diminta, kita harus memilih 4 dari 7 anggota M.

Karena {1, 2, 3, 4} = {4, 3, 2, 1}, jadi urutan tidak diperhatikan. Sehingga kita akan menggunakan rumus kombinasi untuk memilih 4 dari 7.

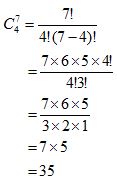
Jadi, himpunan bagian M yang banyak anggotanya ada 4 ada 35 himpunan bagian.

6. Jika diberikan sebuah persamaan

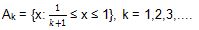
Berapakah hasil

Pembahasan

Untuk mengerjakan soal ini, kita harus memahami bentuk persamaan . Berdasarkan bentuk tersebut maka kita dapat menuliskan = A₁ U A₂ U…

Dari bentuk di atas, kita dapat memasukkan nilai k=1,2,3,..

Kita masukkan nilai k=1

A₁ = {x: ½ ≤ x ≤ 1}

Kita masukkan nilai k=2

A₂ = {x: ⅓ ≤ x ≤ 1}

Kita masukkan nilai k=3

A₃ = {x: ¼ ≤ x ≤ 1}

Berdasarkan hasil di atas, jika kita memasukkan nilai k=∞, maka hasil yang didapat seperti berikut

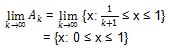
7. Himpunan Y memenuhi sebuah persamaan sebagai berikut {1,2} ⊆ Y ⊆ {1,2,3,4,5}. Tentukan banyaknya himpunan Y dari persamaan tersebut.

Pembahasan

Untuk mengerjakan soal di atas, kita perlu melihat batas bawah dan batas atas dari persamaan yang di berikan.

Pada soal di atas, batas bawah yang tersedia adalah 2 sedangkan batas atas adalah 5. Sehingga, himpunan anggota Y minimal ada 2 anggota dari himpunan {1,2}.

Kita dapat mengerjakan soal tersebut dengan 4 kemungkinan seperti di bawah ini.

Kemungkinan 1

Himpunan anggota Y hanya terdiri dari 2 anggota, maka kita tidak dapat memilih himpunan 3,4,5.

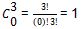
Kemungkinan 2

Himpunan anggota Y hanya terdiri dari 3 anggota, maka kita dapat memilih himpunan 3,4,5.

Kemungkinan 3

Himpunan anggota Y hanya terdiri dari 4 anggota, maka kita dapat memilih himpunan 2, 3,4,5.

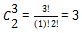
Kemungkinan 4

Himpunan anggota Y hanya terdiri dari 5 anggota, maka kita dapat memilih semua anggota himpunan {1,2} dan {1,2,3,4,5}.

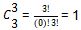
Banyaknya anggota himpunan yang memenuhi persamaan di atas sebanyak 1 + 3 + 3 + 1 = 8.

8. Sebuah himpunan A = {4} dan B = {b | b² – 16 = 0, b>0}, apakah dapat dikatakan bahwa A = B.

Kesimpulan

• Himpunan merupakan kumpulan objek yang didefinsikan secara jelas (terukur).
• Himpunan kosong merupakan himpunan yang tidak memiliki anggota.
• Himpunan semesta merupakan himpunan yang terditi dari seluruh objek yang sedang dibicarakan.
• Himpunan bagian merupakan himpunan yang anggota-anggotanya merupakan elemen dari himpunan semesta.
• Operasi dalam himpunan ada dua yaitu operasi irisan dan gabungan.
• Himpunan penyelesaian merupakan himpunan dengan anggotanya merupakan penyelesaian atau solusi dari suatu permasalahan.

Demikian penjelasan mengenai himpunan. Semoga bermanfaat. Baca juga Bilangan Bulat.