Pengertian Trigonometri
Trigonometri merupakan cabang dari ilmu matematika yang mempelajari hubungan antara panjang dan sudut segitiga, biasanya digunakan dalam membuat desain bangunan, pembuatan jembatan, dan pada bidang astronomi. Pelajari lebih lanjut tentang Definisi Trigonometri.
Sedangkan limit trigonometri merupakan nilai paling dekat dari suatu sudut. Istilah-istilah yang ada dalam trigonometri yaitu sinus (sin), cosinus (cos), tangen (tan), secan (sec), cosecan (csc), dan cotangent (ctg).
Pada saat menentukan nilai dari suatu limitnya, beberapa cara/metode yang sering dipakai adalah substitusi, pemfaktoran, turunan, dan kali sekawan.
Dalam trigonometri, terdapat beberapa rumus yang berbentuk seperti di bawah ini
1. Rumus kebalikan
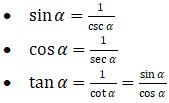
2. Rumus identitas
- sin2α + cos2α = 1
- 1 + cot2α = csc2α
- 1 + tan2α = sec2α
3. Rumus jumlah dan selisih trigonometri
- sin (α + β) = sin α cos β + cos α sin β
- sin (α – β) = sin α cos β – cos α sin β
- cos (α + β) = cos α cos β – sin α sin β
- cos (α – β) = cos α cos β + sin α sin β
4. Rumus perkalian
- 2 cos α cos β = cos (α + β) + cos (α – β)
- 2 cos α sin β = sin (α + β) – sin (α – β)
- 2 sin α cos β = sin (α + β) + sin (α – β)
- – 2 sin α sin β = cos (α + β) – cos (α – β)
5. Sudut rangkap
- sin 2α = 2 sin α cos α
- cos 2α = 1 – 2 sin2α = cos2α – sin2α
- tan 2α =

- cot 2α =

Turunan Trigonometri
| f (x) | f’(x) |
| sin x | cos x |
| cos x | – sin x |
| tan x | sec2 x |
| cot x | – csc2 x |
| sec x | sec x tan x |
| csc x | – csc x cot x |
Keenam jenis rumus di atas merupakan hal yang mendasar dari materi trigonometri, karena hampir setiap soal yang menyangkut geometri pasti menggunakan rumus-rumus tersebut.
Limit Fungsi Trigonometri
Sama halnya dengan limit trigonometri, limit fungsi trigonometri merupakan nilai paling dekat dari suatu sudut pada fungsi trigonometri. Dalam penghitungannya, terdapat 2 (dua) teorema yang menjadi dasar dari limit fungsi trigonometri seperti di bawah ini:
Teorema 1 (hanya berlaku pada saat x → 0)
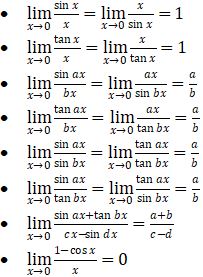
Teorema 2 (hanya berlaku pada saat x → c, Ɐc ∈ R)
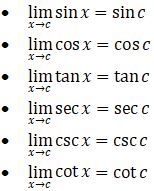
Menggunakan 2 (dua) teorema di atas, kita dapat mencari nilai dari sebuah limit trigonometri dengan lebih mudah.
Dalam sebuah soal limit fungsi trigonometri pula, biasanya menggunakan sudut-sudut istimewa yang nilainya tidak rumit.
Sudut-sudut istimewa dalam trigonometri yaitu 0o, 30o, 45o, 60o, 90o. Agar lebih mudah dalam memahami sudut istimewa, perhatikan tabel sudut istimewa dari 4 kuadran di bawah ini:
Kuadran 1
| 0o | 30o | 45o | 60o | 90o | |
| sin α | 0 | ½ | ½√2 | ½√3 | 1 |
| cos α | 1 | ½√3 | ½√2 | ½ | 0 |
| tan α | 0 | ⅓√3 | 1 | √3 | – |
| csc α | – | 2 | √2 | ⅔√3 | 1 |
| sec α | 1 | ⅔√3 | √2 | 2 | – |
| cot α | – | √3 | 1 | ⅓√3 | 0 |
Kuadran 2
| 90o | 120o | 135o | 150o | 180o | |
| sin α | 1 | ½√3 | ½√2 | ½ | 0 |
| cos α | 0 | -½ | -½√2 | -½√3 | -1 |
| tan α | – | -√3 | -1 | -⅓√3 | 0 |
| csc α | 1 | ⅔√3 | √2 | 2 | – |
| sec α | – | – 2 | -√2 | -⅔√3 | -1 |
| cot α | 0 | -⅓√3 | -1 | -√3 | – |
Kuadran 3
| 180o | 210o | 225o | 240o | 270o | |
| sin α | 0 | -½ | -½√2 | -½√3 | -1 |
| cos α | -1 | -½√3 | -½√2 | -½ | 0 |
| tan α | 0 | ⅓√3 | 1 | √3 | – |
| csc α | – | -2 | -√2 | -⅔√3 | -1 |
| sec α | -1 | -⅔√3 | -√2 | – 2 | – |
| cot α | – | -√3 | 1 | -⅓√3 | 1 |
Kuadran 4
| 270o | 300o | 315o | 330o | 360o | |
| sin α | -1 | -½√3 | -½√2 | -½ | 0 |
| cos α | 0 | ½ | ½√2 | ½√3 | 1 |
| tan α | – | -√3 | -1 | -⅓√3 | 0 |
| csc α | -1 | -⅔√3 | -√2 | -2 | – |
| sec α | – | 2 | √2 | ⅔√3 | -1 |
| cot α | 1 | -⅓√3 | -1 | -√3 | – |
Setelah mempelajari tabel sudut istimewa di atas, telah dimengerti bahwa terdapat beberapa sudut istimewa di setiap kuadran dan jika diperhatikan lebih lanjut maka akan terlihat bahwa setiap kuadran memiliki keterkaitan dan/atau kemiripan satu sama lain.
Agar lebih memahami materi trigonometri, perhatikan beberapa contoh soal berikut pembahasannya di bawah ini:
Contoh Soal Limit Trigonometri

4. Diberikan sebuah bentuk limit trigonometri sebagai berikut
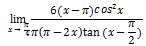
Tentukan hasil operasi limit di atas!
Untuk mengerjakan soal ini, kamu harus melihat kembali identitas trigonometri dan teorema limit trigonometri.
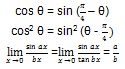
Dari indentitas trigonometri dan teorema limit trigonometri di atas, kita dapat menyelesaikan soal limit trigonometrinya.
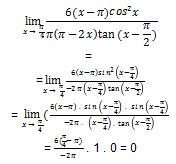
Jadi, hasilnya adalah
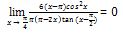
5. Terdapat sebuah fungsi campuran seperti di bawah ini
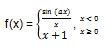
Berapakah nilai a jika limit di x = 0?
Pertama, untuk mengerjakan soal ini, kita harus memberlakukan batas limit kanan dan kiri.
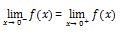
- Uji nilai pada ruas kiri
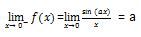
- Uji nilai pada ruas kanan
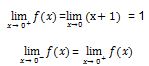
a = 1
Untuk memenuhi persamaan di atas, maka nilai a=1.
6. Berapakah nilai a dan b dalam limit trigonometri di bawah ini
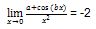
Pertama, untuk mengerjakan soal tersebut, kita harus membuat . Hal ini bertujuan untuk mendapatkan nilai a pada persamaan tersebut.
Sehingga kita dapat menuliskan persamaannya seperti berikut.
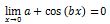
a + cos (0.b) = 0
a + cos 0o = 0
a + 1 = 0
a = -1
Setelah mendapatkan nilai a, maka kita bisa memasukkan nilai a ke dalam persamaan tersebut sehingga membentuk
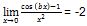
Namun, jika kita memasukkan nilai x=0, maka hasil yang di dapatkan adalah bentuk tak tentu.
Kita dapat menggunakan dalil L’Hospital bertingkat untuk mendapatkan bentuk persamaan yang lebih baik.
Dalil L’Hospital 1
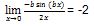
Persamaan di atas, disederhanakan kembali menggunakan Dalil L’Hospital.
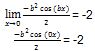
-b2 = -4
b = 2
Nilai a dan b yang memenuhi untuk persamaan limit trigonometri di atas adalah a=-1 dan b=2. Namun untuk mendapatkan hasil yang lebih objektif, b= ±2.
7. Tentukan hasil operasi limit trigonometri berikut
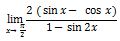
Untuk mengerjakan persamaan limit trigonometri di atas, kita harus mengingat identitas trigonometri.
Sehingga dapat memudahkan untuk mengerjakan soal limit trigonometri di atas.
1 – sin 2x = sin2 x – 2 sin x cos x + cos2 x
1 – sin 2x = (sin x – cos x)2
Kita bisa memasukkan persamaan di atas ke dalam soal, sehingga bentuknya seperti di bawah ini.
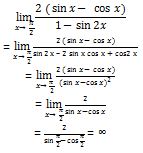
Hasil dari operasi limit trigonometri tersebut adalah tidak terhingga.
8. Diberikan bentuk limit trigonometri seperti di bawah ini
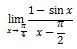
Berapakah hasil operasi limit trigonometri tersebut?
Untuk mengerjakan soal jenis seperti ini, kita perlu untuk melakukan perkalian silang pada pecahan tersebut untuk mendapatkan bentuk yang sederhana.
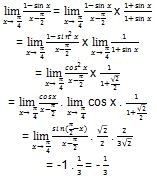
Hasil akhir operasi hitung fungsi limit trigonometri di atas adalah -⅓.
Jika sudah memahami contoh soal di atas, maka diharapkan kita dapat mencoba soal yang lebih menantang lagi agar semakin menambah pemahaman akan materi limit fungsi trigonometri. Baca juga Identitas Trigonometri.
