Pernahkah kalian mendengar trigonometri?
Kata trigonometri biasanya sering ditemui dalam pembelajaran matematika, khususnya mengenai sisi dan sudut segitiga.
Untuk mempelajari lebih jauh mengenai trigonometri, mari kita simak penjelasan berikut ini
Definisi Trigonometri
Trigonometri berasal dari kata trigonos (segitiga) dan metros (ukuran).
Trigonometri adalah salah satu cabang ilmu dalam matematika yang mempelajari mengenai ukuran sisi dan sudut pada segitiga.
Awalnya, trigonometri hanya berkaitan dengan perbandingan sisi dan sudut pada segitiga siku-siku. Namun seiring perkembangan zaman, trigonometri terus berkembang hingga sekarang.
Trigonometri dalam kehidupan sehari-hari
Penerapan trigonometri dalam berbagai bidang diantaranya adalah penggunaan trigonometri dalam mencari ketinggian bangunan maupun pegunungan, penggunaan trigonometri dalam menghitung ketinggian gelombang air laut, menghitung ketinggian suatu pohon, selain itu, trigonometri juga dapat digunakan dalam mencari jarak antar benda benda luar angkasa.
Perbandingan trigonometri
Beberapa hal dasar yang harus kita ketahui tentang trigonometri salah satunya adalah mengenai perbandingan trigonometri. Untuk lebih jelasnya melalui gambar dibawah ini.
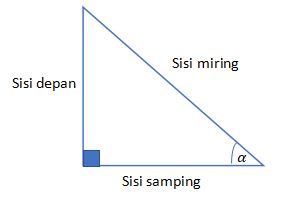

Tabel nilai fungsi trigonometri sudut istimewa
Untuk beberapa sudut istimewa, nilai fungsi trigonometrinya dituliskan dalam tabel berikut ini
| 0 ̊ | 30 ̊ | 45 ̊ | 60 ̊ | 90 ̊ | |
| Sin | 0 | 1/2 | 1/2 √2 | 1/2 √3 | 1 |
| Cos | 1 | 1/2 √3 | 1/2 √2 | 1/2 | 0 |
| tan | 0 | 1/3 √3 | 1 | √3 | ∞ |
Identitas trigonometri
Selain perbandingan trigonometri, ada juga hal yang tidak kalah penting, yaitu identitas trigonometri. Identitas trigonometri tersebut diantaranya
sin²a+cos²a=1
1+tan²a=sec²a
1+cot²a=csc²a
Pelajari lebih lanjut di Identitas Trigonometri.
Aturan sinus dan cosinus
Diketahui terdapat segitiga sembarang ABC seperti pada gambar, sehingga
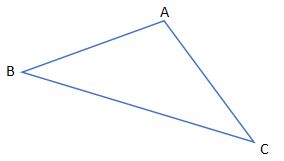
Aturan sinus : pada segitiga sembarang ABC, perbandingan antara panjang sisi dengan sin sudut yang berhadapan dengan sisi tersebut memiliki nilai yang sama
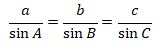
Aturan cosinus : untuk segitiga sembarang ABC, berlaku
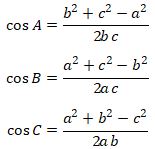
Pelajari lebih lanjut di Aturan Sinus dan Cosinus
Contoh Soal Trigonometri dan Jawabannya
Diberikan sebuah segitiga sembarang dengan besar sudut A adalah 150 derajat. Panjang sisi b adalah 15 cm dan c adalah 8 cm. Tentukan luas segitiga ABC dengan pendekatan cosinus
Dalam menjawab soal ini, kita perlu untuk menggambarkan bentuk segitiga sesuai penjelasan dalam soal. Hal ini memudahkan kita untuk memahami soal serta menentukan rumus luas segitiga yang tepat. Gambar segitiga bisa dilihat di bawah ini yang sudah disesuaikan dengan penjelasan soal tersebut.
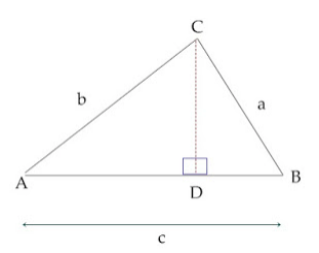
Dalam gambar segitiga di atas, sudut A adalah 150o, sedangkan sisi b memiliki panjang 15 cm dan sisi c memiliki panjang 8 cm. Dikarenakan A diapit oleh sisi C dan B, maka kita dapat menghitung luas segitiga menggunakan sisi b dan c seperti penjelasan di bawah ini.
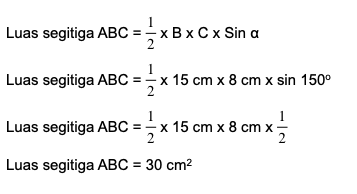
Sehingga luas segitiga ABC di atas adalah 30 cm2
Diberikan sebuah koordinat titik B(-2√2, -2√2). Tentukan koordinat kutub titik B
Untuk mengerjakan soal trigonometri di atas, kita harus memahami 2 hal yaitu koordinat B dan koordinat kutub B. Dijelaskan bahwa koordinat B adalah (-2√2, -2√2). Sehingga kita dapat mengetahui nilai x = -2√2 dan nilai y = -2√2.
Koordinat kutub terdiri dari nilai r dan θ. Pertama, kita bisa mencari nilai r kemudian dilanjutkan dengan nilai θ. Untuk penjelasan lengkapnya, dapat menyimak penjabaran trigonometri di bawah ini.
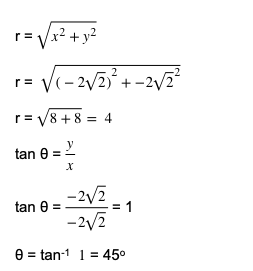
Sehingga koordinat kutub B (r, θ) = (4, 45o).
Tentukan nilai cos a pada gambar segitiga berikut
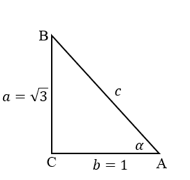
Dalam mengerjakan soal segitiga di atas, kita bisa menggunakan teorema phytagoras.
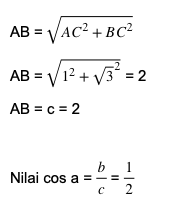
Diberikan sebuah tan α = 1 / α dimana 0 < α < 90o. Tentukan hasil operasi perhitungan dari cos α – 1 / (sin α) adalah
Diketahui bahwa nilai tan α = 1 / α , kita bisa mengingat tan merupakan perbandingan antara nilai depan dengan samping atau sisi tinggi dengan sisi alas. Sehingga, tinggi segitiga adalah 1 dan sisi alas adalah α.
Kita dapat menggunakan teorema phytagoras untuk mendapatkan nilai samping seperti contoh soal trigonometri sebelumnya.
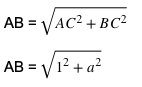
Untuk mendapatkan nilai cos α, dapat menggunakan perbandingan nilai alas dengan nilai samping. Sedangkan untuk sin α, kita dapat menggunakan perbandingan tinggi segitiga dengan samping. Sehingga, kita bisa menuliskan bentuknya seperti di bawah ini.
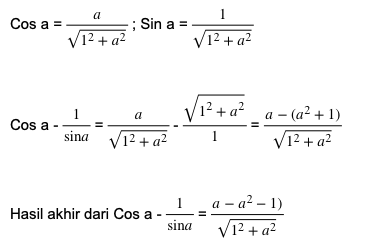
Demikian pembahasan tentang trigonometri dan contoh soalnya. Semoga bermanfaat.
